• DG Betting Blog
We had a tough time with our top 20 bets in 2018, and this annoying trend has continued into the start of this year. While we think that this poor performance is at least in part
the product of bad variance, it has forced us to re-evaulate our betting strategy.
For full-field events on the PGA Tour, our model typically shows value on anywhere from 20-40 Top 20 bets (likely depends on various factors, mostly to do with the bookmaker's behavior). This week at the Genesis Open for example, we have 31 positive expected value top 20 bets according to our model. A real concern with any model-based betting strategy is, obviously, that your model is inaccurate to some degree. Model inaccuracy is problematic because it means that at least part of the positive discrepancies you find between the bookmaker's odds and your own does not reflect true positive expected value. A simple way to allow for some model error is to have a "threshold rule" for the bets you act on: for example, maybe you only place a bet if it has at least 10% expected value (i.e. it is expected to return $0.1 per $1 bet). The goal with these rules is to provide a sufficient buffer to ensure that the bets you take are still positive EV, even if your model probabilities are slightly incorrect (which they are). We currently employ threshold rules, but haven't really evaluated whether these thresholds made sense. Let's do a quick exercise to get a sense of what a reasonable threshold rule should be.
If you've read our blog on model methodology, then you know our general approach is to model golf scores in a given round as normally distributed with some mean and variance. Let's suppose that our estimate of a golfer's mean is itself normally distributed with mean equal to our estimate, and standard deviation equal to 0.25. For example, we estimate Dustin Johnson to be 2.2 strokes better than an average PGA Tour pro; therefore we would be be fairly confident that Johnson's "true current ability" lies somewhere between 1.95 and 2.45, and very confident that it lies somewhere between 1.7 and 2.7 (recall the property of normal distributions: ~68% of the data is within 1 standard deviation of the mean, ~95% is within 2 standard deviations). Obviously, the standard deviation assumed here is critical; our guess is that 0.25 is likely a lower bound. For example, if you were trying to estimate a population mean from a sample of size n where each observation is pulled from a Normal(0, 2.75) distribution, the standard deviation of your estimate would be 2.75/sqrt(n). So, for an n of 100, the standard deviation would be 0.275. Note that the standard deviation of a golfer's scores, assuming constant ability over time (this is a loaded statement), is roughly 2.75. I would say 0.25 is a lower bound because it only really accounts for sampling uncertainty - it does not account for the fact that your entire modelling strategy may be incorrect.
The exercise we do is the following: we treat our current model predictions as "truth", and then we apply a normally distributed shock (with mean 0 and standard deviation 0.25) to each of these predictions. With these new "noisy" predictions, we can then calculate our percieved expected value (using these noisy predictions) and compare that to the "true" expected value (obtained by using our original predictions of golfer ability). Here's what we find: with a threshold rule of 10% and using the noisy predictions to obtain our Top 20 probabilities, we find 33 bets worth taking (i.e. above 10% EV). The percieved expected value of these bets is, on average, 34%. The "true" expected value, using probabilities derived from our original predictions, is just 10% on average. Further, 11 of these bets actually have negative "true" expected value. This is disconcerting, to say the least. Not only are we only getting 1/3 of the positive expected value we think we are getting, we are also placing several bets that are negative expected value!
A problem with this analysis is that we are holding offered odds fixed. When a golfer gets a big shock to their ability (i.e. an extreme draw from the noise distribution), it's likely that this shock would affect all models, including the bookmaker's, and so their odds would reflect this. This would in turn affect which bets we find the most positive expected value on with our "noisy" predictions. This is probably not clear, but an example of this could be that Bryson DeChambeau has played way above his true ability over the last 50 rounds. All models will reflect this "sampling noise". What really matters here are differences between our model and the bookmaker's model. If both models underestimate or overestimate a player's true ability level by the same amount, it doesn't matter for betting outcomes because a bet will not be placed regardless. Therefore, any type of model error that is common to both models should not be incorporated into the noise term we apply. In this sense the standard deviation of 0.25 for the noise term may be too high.
This exercise indicates that, given the assumptions we've made, a threshold of 10% is not sufficient. We do not want to be making bets that have a reasonable chance of being negative expected value. The influence of noise is especially problematic on bets with very long odds. For example, Keith Mitchell and Matt Kuchar both had shocks to their expected scoring averages of +0.33; this moved the expected value on a Top 20 Mitchell bet (odds of 10.0) from 32% to 88%, while it moved the Top 20 Kuchar bet (odds of 2.75) from -13% to 11%. I haven't thought enough about this to have an exact explanation for the relationship between the odds provided and the influence of noise, but it is clear that the introduction of noise affects things much more the longer are the odds offered. This isn't too surprising, given that the same discrepancy in terms of probability provides more expected value the longer the odds; but it's also true that the same scoring average shock affects longer odds golfers T20 probability less. It's also worth pointing out that for any outright finish bets (top 20, top 5, etc.), the effect of noise is magnified by the fact that model error for any individual golfer affects every other golfer. This is in contrast to bets involving just 2 or 3 players, such as tournament matches, which evidently can only be influenced by errors in the ability estimates of the players involved in the match.
Moving forward, we will be adopting a higher threshold for expected value (~20%) on Top 20 bets. It would require a little bit of work, but we should make this threshold vary with the odds being offered (i.e. higher threshold for longer odds)
The Cliff's notes from this example are: 1) We added a model error term that results in many of our model's projected abilities for golfers to be off by at least 0.25 strokes (units are in strokes per round), 2) This makes it more likely that the highest expected value bets were in part due to a positive error term shock; 3) This modelling error affects all bets, but especially those with longer odds and more players involved in the outcome (e.g. Top 20s); 4) Using a standard deviation of 0.25 for the error distribution in 1), and using Top 20 bets as an example, you may only have about 1/4 or 1/3 of the expected value you think you have, and there may be several bets where the model indicates significant positive expected value, but in actuality they are negative expected value propositions. None of this is particularly novel, but it was helpful to put some numbers behind these thoughts, even if they are just rough guesses for now. The critical question here is what a reasonable standard deviation is for the assumption in 1). This requires coming up with a description of how your model and the bookmaker's odd setting procedure are related; something that is well outside the scope of this blog post.
Another useful exercise, which can be related to what was written above, is to simulate the distribution of profit given the bets we are making. The purpose of doing this is to understand what kind of variation in profit is possible under various assumptions about the world (e.g. whether your model is correct, or not). Shown below are two profit distributions. Both distributions are for 10-week profit making 20 bets per week (so, 200 bets total). We are just using the Genesis Open bets for every week. In the first plot, we use our model's abilities and the 20 highest EV bets this week to run 20,000 simulations of 10 weeks worth of bets. The resulting distribution shows the possible profit paths and their frequency of occurence if our model were the truth. The second plot shows the same simulation exercise, except we use the 20 highest EV bets using the model predictions with noise added to them. Therefore, we are again assuming our model is truth to simulate, but we placed bets according to the expected value derived from our model with errors added to the golfer ability estimates.
For full-field events on the PGA Tour, our model typically shows value on anywhere from 20-40 Top 20 bets (likely depends on various factors, mostly to do with the bookmaker's behavior). This week at the Genesis Open for example, we have 31 positive expected value top 20 bets according to our model. A real concern with any model-based betting strategy is, obviously, that your model is inaccurate to some degree. Model inaccuracy is problematic because it means that at least part of the positive discrepancies you find between the bookmaker's odds and your own does not reflect true positive expected value. A simple way to allow for some model error is to have a "threshold rule" for the bets you act on: for example, maybe you only place a bet if it has at least 10% expected value (i.e. it is expected to return $0.1 per $1 bet). The goal with these rules is to provide a sufficient buffer to ensure that the bets you take are still positive EV, even if your model probabilities are slightly incorrect (which they are). We currently employ threshold rules, but haven't really evaluated whether these thresholds made sense. Let's do a quick exercise to get a sense of what a reasonable threshold rule should be.
If you've read our blog on model methodology, then you know our general approach is to model golf scores in a given round as normally distributed with some mean and variance. Let's suppose that our estimate of a golfer's mean is itself normally distributed with mean equal to our estimate, and standard deviation equal to 0.25. For example, we estimate Dustin Johnson to be 2.2 strokes better than an average PGA Tour pro; therefore we would be be fairly confident that Johnson's "true current ability" lies somewhere between 1.95 and 2.45, and very confident that it lies somewhere between 1.7 and 2.7 (recall the property of normal distributions: ~68% of the data is within 1 standard deviation of the mean, ~95% is within 2 standard deviations). Obviously, the standard deviation assumed here is critical; our guess is that 0.25 is likely a lower bound. For example, if you were trying to estimate a population mean from a sample of size n where each observation is pulled from a Normal(0, 2.75) distribution, the standard deviation of your estimate would be 2.75/sqrt(n). So, for an n of 100, the standard deviation would be 0.275. Note that the standard deviation of a golfer's scores, assuming constant ability over time (this is a loaded statement), is roughly 2.75. I would say 0.25 is a lower bound because it only really accounts for sampling uncertainty - it does not account for the fact that your entire modelling strategy may be incorrect.
The exercise we do is the following: we treat our current model predictions as "truth", and then we apply a normally distributed shock (with mean 0 and standard deviation 0.25) to each of these predictions. With these new "noisy" predictions, we can then calculate our percieved expected value (using these noisy predictions) and compare that to the "true" expected value (obtained by using our original predictions of golfer ability). Here's what we find: with a threshold rule of 10% and using the noisy predictions to obtain our Top 20 probabilities, we find 33 bets worth taking (i.e. above 10% EV). The percieved expected value of these bets is, on average, 34%. The "true" expected value, using probabilities derived from our original predictions, is just 10% on average. Further, 11 of these bets actually have negative "true" expected value. This is disconcerting, to say the least. Not only are we only getting 1/3 of the positive expected value we think we are getting, we are also placing several bets that are negative expected value!
A problem with this analysis is that we are holding offered odds fixed. When a golfer gets a big shock to their ability (i.e. an extreme draw from the noise distribution), it's likely that this shock would affect all models, including the bookmaker's, and so their odds would reflect this. This would in turn affect which bets we find the most positive expected value on with our "noisy" predictions. This is probably not clear, but an example of this could be that Bryson DeChambeau has played way above his true ability over the last 50 rounds. All models will reflect this "sampling noise". What really matters here are differences between our model and the bookmaker's model. If both models underestimate or overestimate a player's true ability level by the same amount, it doesn't matter for betting outcomes because a bet will not be placed regardless. Therefore, any type of model error that is common to both models should not be incorporated into the noise term we apply. In this sense the standard deviation of 0.25 for the noise term may be too high.
This exercise indicates that, given the assumptions we've made, a threshold of 10% is not sufficient. We do not want to be making bets that have a reasonable chance of being negative expected value. The influence of noise is especially problematic on bets with very long odds. For example, Keith Mitchell and Matt Kuchar both had shocks to their expected scoring averages of +0.33; this moved the expected value on a Top 20 Mitchell bet (odds of 10.0) from 32% to 88%, while it moved the Top 20 Kuchar bet (odds of 2.75) from -13% to 11%. I haven't thought enough about this to have an exact explanation for the relationship between the odds provided and the influence of noise, but it is clear that the introduction of noise affects things much more the longer are the odds offered. This isn't too surprising, given that the same discrepancy in terms of probability provides more expected value the longer the odds; but it's also true that the same scoring average shock affects longer odds golfers T20 probability less. It's also worth pointing out that for any outright finish bets (top 20, top 5, etc.), the effect of noise is magnified by the fact that model error for any individual golfer affects every other golfer. This is in contrast to bets involving just 2 or 3 players, such as tournament matches, which evidently can only be influenced by errors in the ability estimates of the players involved in the match.
Moving forward, we will be adopting a higher threshold for expected value (~20%) on Top 20 bets. It would require a little bit of work, but we should make this threshold vary with the odds being offered (i.e. higher threshold for longer odds)
The Cliff's notes from this example are: 1) We added a model error term that results in many of our model's projected abilities for golfers to be off by at least 0.25 strokes (units are in strokes per round), 2) This makes it more likely that the highest expected value bets were in part due to a positive error term shock; 3) This modelling error affects all bets, but especially those with longer odds and more players involved in the outcome (e.g. Top 20s); 4) Using a standard deviation of 0.25 for the error distribution in 1), and using Top 20 bets as an example, you may only have about 1/4 or 1/3 of the expected value you think you have, and there may be several bets where the model indicates significant positive expected value, but in actuality they are negative expected value propositions. None of this is particularly novel, but it was helpful to put some numbers behind these thoughts, even if they are just rough guesses for now. The critical question here is what a reasonable standard deviation is for the assumption in 1). This requires coming up with a description of how your model and the bookmaker's odd setting procedure are related; something that is well outside the scope of this blog post.
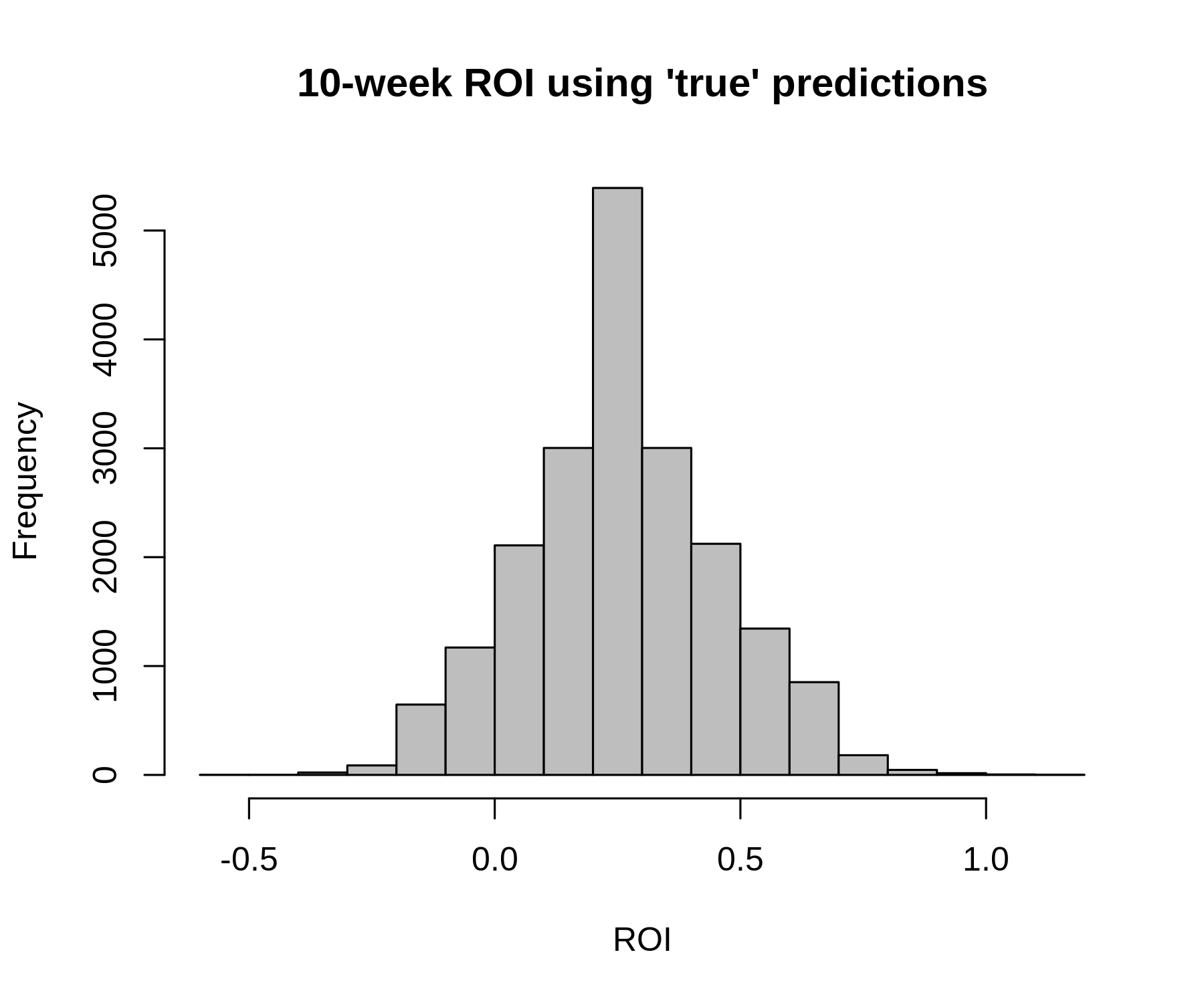
Another useful exercise, which can be related to what was written above, is to simulate the distribution of profit given the bets we are making. The purpose of doing this is to understand what kind of variation in profit is possible under various assumptions about the world (e.g. whether your model is correct, or not). Shown below are two profit distributions. Both distributions are for 10-week profit making 20 bets per week (so, 200 bets total). We are just using the Genesis Open bets for every week. In the first plot, we use our model's abilities and the 20 highest EV bets this week to run 20,000 simulations of 10 weeks worth of bets. The resulting distribution shows the possible profit paths and their frequency of occurence if our model were the truth. The second plot shows the same simulation exercise, except we use the 20 highest EV bets using the model predictions with noise added to them. Therefore, we are again assuming our model is truth to simulate, but we placed bets according to the expected value derived from our model with errors added to the golfer ability estimates.
(Ignore the non-continuous shape: this occured because wagers were set equal to 1 divided by the odds, and so there were only so
many different profit paths that were possible). In the first case, where we placed bets on the 20 highest expected value plays as indicated by our model and we
simulated outcomes using our model odds, the average 10-week ROI (defined as total profit divided by total amount wagered) is
26%; in 9.7% of simulations ROI is negative. This last point speaks to the variance inherent to Top 20 bets.
In the second case, where we placed bets on the 20 highest expected value plays using our noisy predictions, but we again simulated outcomes using our model probabilities, the average 10-week ROI is 6.3%. In 34.9% of simulations ROI is negative.
The relationship between ROI in the two cases is expected given what was outlined above; we are only getting about 20-30% of the expected value relative to the best-case scenario (i.e. the model used to make your bets is the truth). The probability of having a negative ROI through 10 weeks is also pretty interesting. Moving forward we will give this some more thought; the key for this analysis to be useful is understanding what a reasonable value is for the standard deviation of the shock to the "true" model predictions.
In the second case, where we placed bets on the 20 highest expected value plays using our noisy predictions, but we again simulated outcomes using our model probabilities, the average 10-week ROI is 6.3%. In 34.9% of simulations ROI is negative.
The relationship between ROI in the two cases is expected given what was outlined above; we are only getting about 20-30% of the expected value relative to the best-case scenario (i.e. the model used to make your bets is the truth). The probability of having a negative ROI through 10 weeks is also pretty interesting. Moving forward we will give this some more thought; the key for this analysis to be useful is understanding what a reasonable value is for the standard deviation of the shock to the "true" model predictions.