This off-season was nice in that we didn't really do anything resembling an overhaul to the model like we did in 2020 or 2021. However there was one interesting change in methodology I want to discuss here. I would consider this change a model "fundamental" in the sense that it affects every prediction and it's not simply about incorporating previously unused data (e.g. accounting for course history).

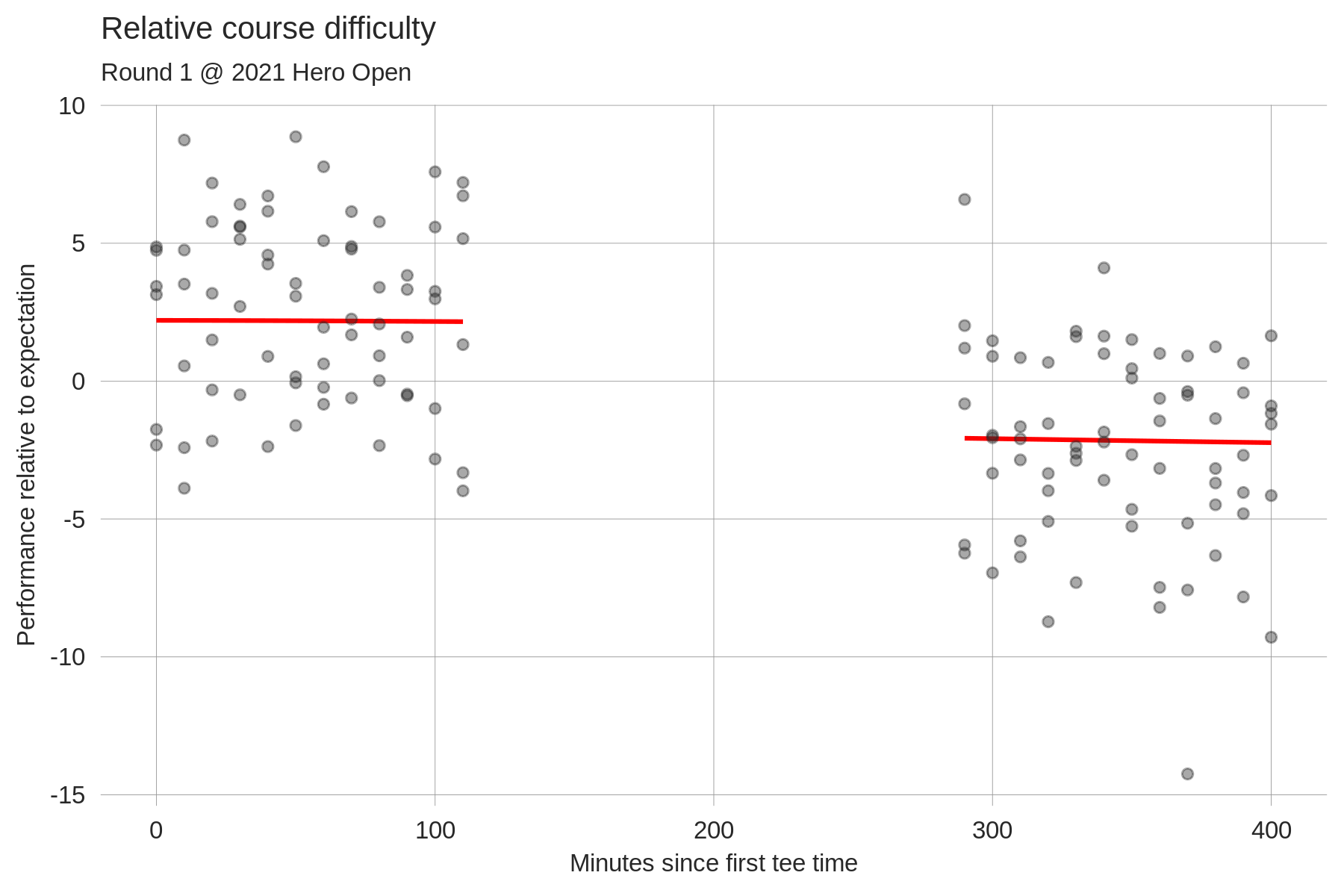
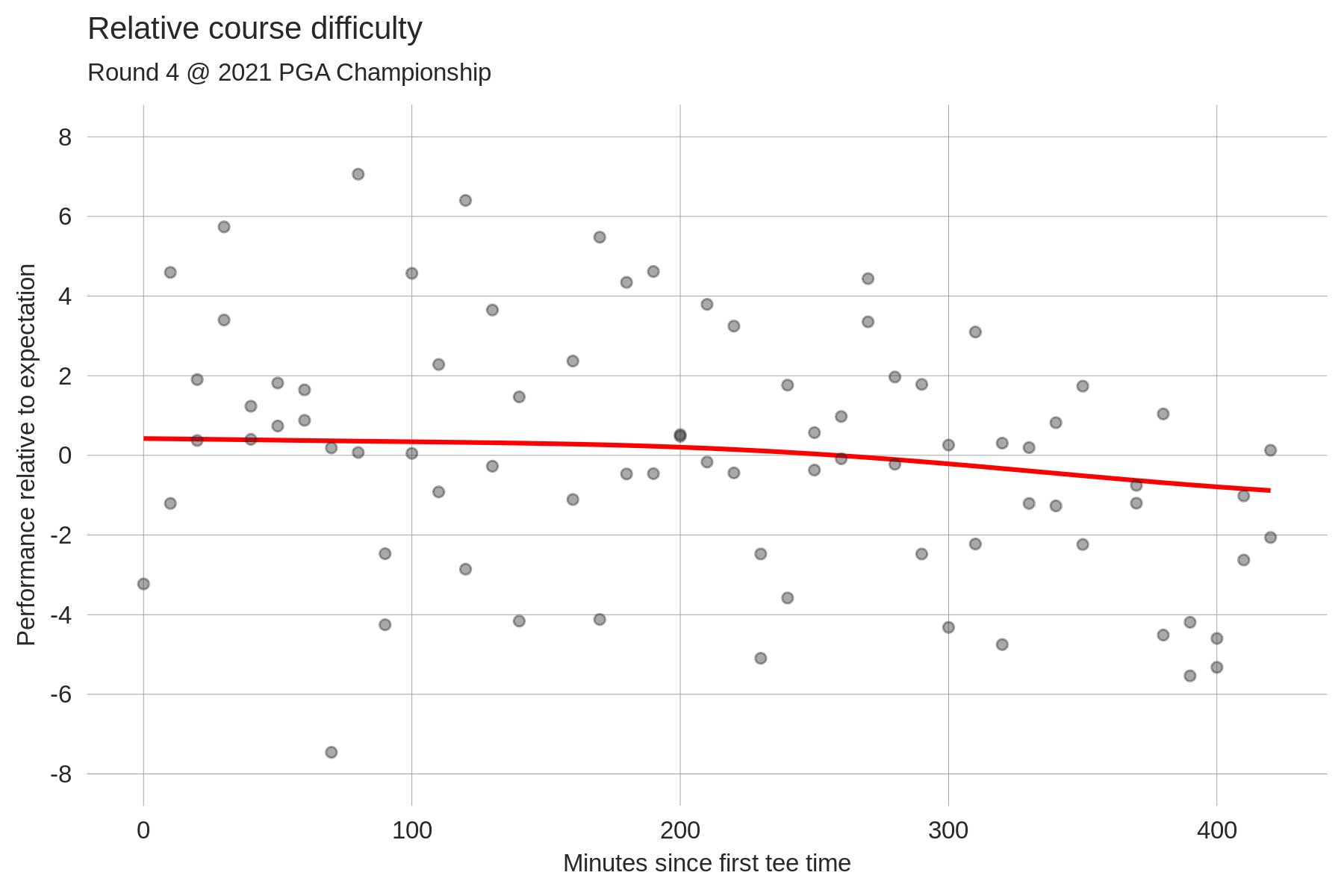
In the current version of the model, a player's so-called baseline skill is estimated by averaging their historical true strokes-gained values using various weighting schemes. Recall that baseline skill should be thought of as a player's predicted skill at a neutral course; our final predictions at a specific course then tack on course-specific adjustments to this baseline. True strokes-gained, in the form it appears on our website, is less than optimal to estimate baseline skill for two reasons: 1) it assumes that the course played equally difficult for all players within a round, and 2) it doesn't remove course-specific skill adjustments from a player's performance. Point 1 is problematic for obvious reasons: e.g. sometimes the morning wave plays harder than the afternoon wave or vice versa. To adjust for this, in each round we fit golfers' performance relative to expectation as a function of their tee time to get a continuous estimate of course difficulty throughout the day. Here are two examples:



Each data point is a specific golfer's performance relative to our model's expectation, which obviously accounts for their overall skill level but also for their position on the leaderboard at the start of rounds 3 and 4 (e.g. we expect final round leaders on the PGA Tour to perform ~0.4 strokes worse than their skill level). The red fitted line, in theory, tells us about relative course difficulty throughout the day: if the morning golfers on average performed above expectation, a logical explanation for that would be that the course played easier (but, it's not the only explanation). Importantly, this fit is chosen to minimize out-of-sample prediction error. The first plot illustrates what this means in practice: the average residual performance of the morning wave was +2.5 while that of the afternoon wave was -2.47, yielding a raw wave split of 4.97 strokes. The fitted wave split (i.e. the difference in average morning vs. afternoon fitted values) is only 4.3 strokes. Intuitively, because the raw wave split was so large we expect that some of it is due to "luck" rather than actual course difficulty differences, and so the fitted values are regressed slightly towards zero. The second plot shows the course difficulty adjustments for a single, continuous wave of tee times. It's pretty clear to the naked eye that the fitted line doesn't fit this specific set of data as well as it could (to my eye it looks like the fit should decline more at the right end of the plot). Again, this is done so as to maximize out-of-sample predictive power; the poor performances from the late golfers are likely in part due to chance, and so we regress these fitted values slightly towards zero. This is the bias-variance tradeoff in action.

These course difficulty adjustments are always made to be mean-zero within a round because we want the average true SG value for each round to remain unchanged. That is, we first pin down overall course difficulty (or field strength — if you know one you know the other in our setup) for a round using our 2-way fixed effects regression, and then within each round we adjust for relative course difficulty throughout the day.

Over long time horizons you would of course expect that the course difficulty adjustments cancel out for each golfer (i.e. no one should be systematically facing more difficult conditions), but given the higher weight that more recent rounds receive when estimating golfer skill, these adjustments can matter.

The problems that Point 2 creates are more subtle and can be illustrated with an example. Suppose that Bryson DeChambeau plays an event at a course that favours driving distance much less than the typical PGA Tour venue (e.g. Harbour Town). We should expect DeChambeau to play worse here than at a typical PGA Tour course (about 0.5 strokes worse per round given his current skill profile). Therefore if Bryson averages +1.5 true SG at Harbour Town, the value that should actually enter the average used to estimate his baseline skill is +2 (i.e. we need to subtract off his course fit adjustment). From the model's perspective, Bryson's +1.5 true SG performance at Harbour Town equates to a +2 performance at the average PGA Tour course, and it is the latter that should be used to estimate skill at an average, or neutral, PGA Tour course. This adjustment also won't make a huge difference for the skill estimates of most players, but it can matter in the weeks that follow events with extreme course fit profiles. For example, in the first few weeks of 2022 performances from the Mayakoba Classic — played at El Cameleon Golf Club which has a very extreme profile — will be receiving substantial weight when estimating golfers' current skill, and so adjusting for each golfer's fit at El Cameleon will make a difference.

Heading into 2022, here are the 5 largest positive and negative changes in baseline skill after incorporating these adjustments:


Recall that for the course-specific skill adjustments, players who have recently played courses for which they have good fit and/or history will receive negative adjustments to their predicted skill (compared to a model that is not accounting for this). While these adjustments are admittedly small, I think the underlying theory is strong enough to justify the effort required to include them in the model going forward.