Analytics Blog
Analytics Blog
December 18, 2020
How sharp are bookmakers?
-Analyzing matchup and 3-ball odds from the 2019 and 2020 seasons
Since early January 2019, we have collected odds from 106,204 matchups and 3-balls on the PGA and
European Tours. The database spans 11 sportsbooks
and includes opening and closing lines for
72-hole matchups, single-round matchups, and single-round 3-balls.
In this blog we analyze some of this data and see
how our model stacks
up against the bookmakers.
If you are primarily interested in the assessment of our model's performance, you can
skip right to the final section.
In order to make an honest living, a bookmaker's offered odds on a given bet will add up to more than 100%. The amount by which this exceeds 100% is called the overround or the book's margin. This margin differs across books: Pinnacle generally offers odds with the lowest margin, while books like Bet365 and DraftKings are known as higher-margin books. Rather than summarize differences in the average margin, I'll characterize a book's advantage by calculating the average return from a "blind" betting strategy — i.e. betting on all outcomes. (In golf matchups betting, ties are sometimes treated as void — that is, your money from the bet is returned — while other times ties are a loss. The possibility of void bets makes calculation of the margin ambiguous, and I don't want to include the margin from tie bets in this exercise, anyways). The table below shows the average return — profit per dollar bet, or "ROI" — at each listed book from a blind betting strategy (I don't bet on the Tie when it is offered).
A bettor who is betting randomly at Pinnacle can expect to lose
a meager 3.3 cents per dollar bet. Conversely, with that same random strategy at Bet365,
you will be dishing out just over 7 cents on
the dollar! Some of this difference is due to the fact that Bet365 offers 3-ball bets,
which tend to be higher-margin
bets, while Pinnacle does not. However, even after excluding 3-balls, DraftKings and Bet365 have blind returns
below -6%. You may notice that at Pinnacle, for example,
the blind betting return is substantially better than
the typical margin on their bets (~3.7%). This is because ties are void for all bets offered by Pinnacle,
but I still include those ties when calculating the average return [1].
Also included in the table is the so-called "margin-free return" from the same blind betting strategy at each book. This quantity requires some explaining. It will be useful for our purposes in this blog to be able to remove the margin from each bookmaker's odds. The simplest method for doing so is to divide the implied probability by the sum of implied probabilites in the bet. For example, suppose a bookmaker offered odds of 55% and 47% for a matchup where ties are void: the margin-free probabilities would then simply be 55/(55+47) = 53.9% and 46.1%. That is, this method assumes that the bookmaker applied the margin proportionally to each golfer; but of course, we don't know that this is the case. It is now well known that at more extreme odds bookmakers don't allocate margin proportionally; they put proportionally more margin on longshots than on favourites — this phenomenon is known as the favourite-longshot bias. It's a fascinating topic but it's one we won't discuss here. Fortunately, we can test whether our method for removing the margin is reasonable. If, after removing the margin, a blind betting strategy yields an average return of zero, this means that the margin-free odds approximate the actual likelihood of the event occurring (that is, margin-free odds of 65% do in fact happen 65% of the time.) This is a tricky concept to come to terms with; interested readers are referred to the footnotes [2]. Looking at the table, we see that blind returns at each book are near zero, meaning our method for removing the margin is sufficient here. (Because most odds in this database are between 35% and 65%, it appears that the favourite-longshot bias is not playing a large role.)
I have one final preliminary before getting to the more interesting parts of this analysis. The next table displays the distribution of possible returns from betting randomly against Pinnacle at several sample sizes. This gives a sense of how much variation in betting performance is possible due to randomness alone. The data in the table are produced from 2000 simulations at each sample size, where each simulation consists of simulating matchups using Pinnacle's margin-free probability (i.e. if Pinnacle gives a golfer a 45% win probability, they will win ~45% of the time across all simulations). Ties are not possible in the simulations which is why the average return is around -3.7%. Columns 2-6 are the percentiles of the distribution and column 7 is the fraction of returns that were above 0%.
This table is an important one to keep in mind when interpreting the results that
follow. At sample sizes below 5k bets randomness can still play a meaningful role,
and even with 10k bets 2-3% deviations due to chance alone are possible.
In order to make an honest living, a bookmaker's offered odds on a given bet will add up to more than 100%. The amount by which this exceeds 100% is called the overround or the book's margin. This margin differs across books: Pinnacle generally offers odds with the lowest margin, while books like Bet365 and DraftKings are known as higher-margin books. Rather than summarize differences in the average margin, I'll characterize a book's advantage by calculating the average return from a "blind" betting strategy — i.e. betting on all outcomes. (In golf matchups betting, ties are sometimes treated as void — that is, your money from the bet is returned — while other times ties are a loss. The possibility of void bets makes calculation of the margin ambiguous, and I don't want to include the margin from tie bets in this exercise, anyways). The table below shows the average return — profit per dollar bet, or "ROI" — at each listed book from a blind betting strategy (I don't bet on the Tie when it is offered).
| book | # of bets | blind return | margin-free return |
|---|---|---|---|
| 5dimes | 20882 | -4.60% | 0.05% |
| bet365 | 15848 | -7.08% | 0.06% |
| betcris | 8508 | -5.59% | -0.02% |
| betonline | 6798 | -4.88% | 0.05% |
| bovada | 17877 | -6.80% | 0.08% |
| draftkings | 11868 | -7.01% | -0.34% |
| pinnacle | 11434 | -3.31% | -0.01% |
Also included in the table is the so-called "margin-free return" from the same blind betting strategy at each book. This quantity requires some explaining. It will be useful for our purposes in this blog to be able to remove the margin from each bookmaker's odds. The simplest method for doing so is to divide the implied probability by the sum of implied probabilites in the bet. For example, suppose a bookmaker offered odds of 55% and 47% for a matchup where ties are void: the margin-free probabilities would then simply be 55/(55+47) = 53.9% and 46.1%. That is, this method assumes that the bookmaker applied the margin proportionally to each golfer; but of course, we don't know that this is the case. It is now well known that at more extreme odds bookmakers don't allocate margin proportionally; they put proportionally more margin on longshots than on favourites — this phenomenon is known as the favourite-longshot bias. It's a fascinating topic but it's one we won't discuss here. Fortunately, we can test whether our method for removing the margin is reasonable. If, after removing the margin, a blind betting strategy yields an average return of zero, this means that the margin-free odds approximate the actual likelihood of the event occurring (that is, margin-free odds of 65% do in fact happen 65% of the time.) This is a tricky concept to come to terms with; interested readers are referred to the footnotes [2]. Looking at the table, we see that blind returns at each book are near zero, meaning our method for removing the margin is sufficient here. (Because most odds in this database are between 35% and 65%, it appears that the favourite-longshot bias is not playing a large role.)
I have one final preliminary before getting to the more interesting parts of this analysis. The next table displays the distribution of possible returns from betting randomly against Pinnacle at several sample sizes. This gives a sense of how much variation in betting performance is possible due to randomness alone. The data in the table are produced from 2000 simulations at each sample size, where each simulation consists of simulating matchups using Pinnacle's margin-free probability (i.e. if Pinnacle gives a golfer a 45% win probability, they will win ~45% of the time across all simulations). Ties are not possible in the simulations which is why the average return is around -3.7%. Columns 2-6 are the percentiles of the distribution and column 7 is the fraction of returns that were above 0%.
| N | 5th | 25th | 50th | 75th | 95th | fraction > 0% |
|---|---|---|---|---|---|---|
| 100 | -19.83% | -10.53% | -3.57% | 3.22% | 12.55% | 0.364 |
| 500 | -10.83% | -6.73% | -3.86% | -0.74% | 3.61% | 0.201 |
| 1000 | -8.78% | -6.00% | -3.84% | -1.70% | 1.60% | 0.116 |
| 2500 | -7.04% | -5.14% | -3.78% | -2.43% | -0.36% | 0.034 |
| 5000 | -5.92% | -4.64% | -3.72% | -2.83% | -1.55% | 0.003 |
| 10000 | -5.44% | -4.40% | -3.69% | -3.04% | -2.07% | 0.000 |
Which closing line should we trust?
With the boring stuff out of the way, let's start to analyze the quality of bookmakers' odds.
To assess bookmaker quality, I'll borrow a method I first encountered
in work by
Joseph Buchdahl. (I encourage you to read through the entire thing; much
of the analysis here is based off of Buchdahl's work.) The idea is that to compare the odds from different bookmakers, we use one bookmaker's
odds to bet against the others (and vice versa). As a jumping off point
we'll analyze the closing odds from Pinnacle and
DraftKings. (It's important to note that our "opening" and "closing" odds
are not the official opening and closing lines, but rather
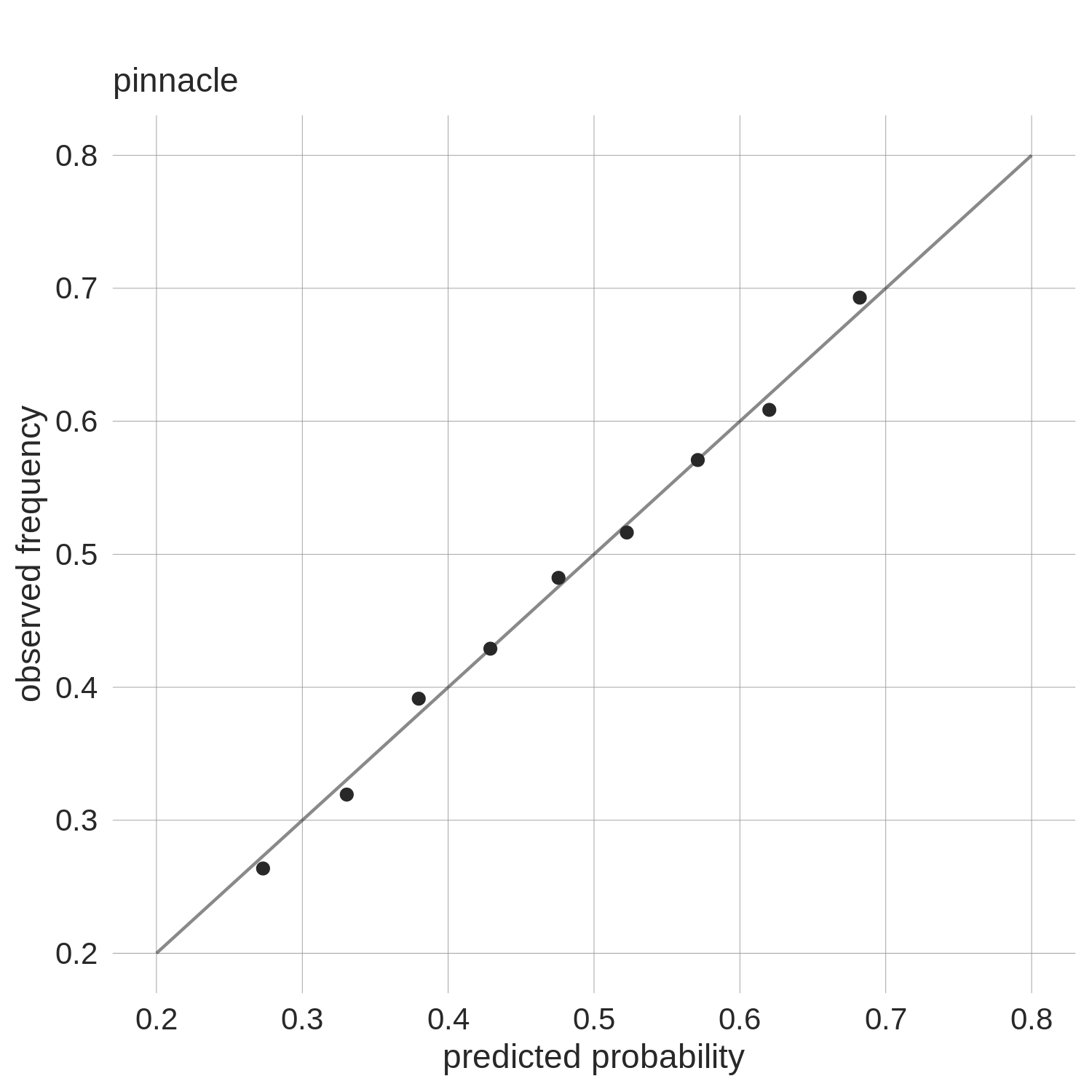
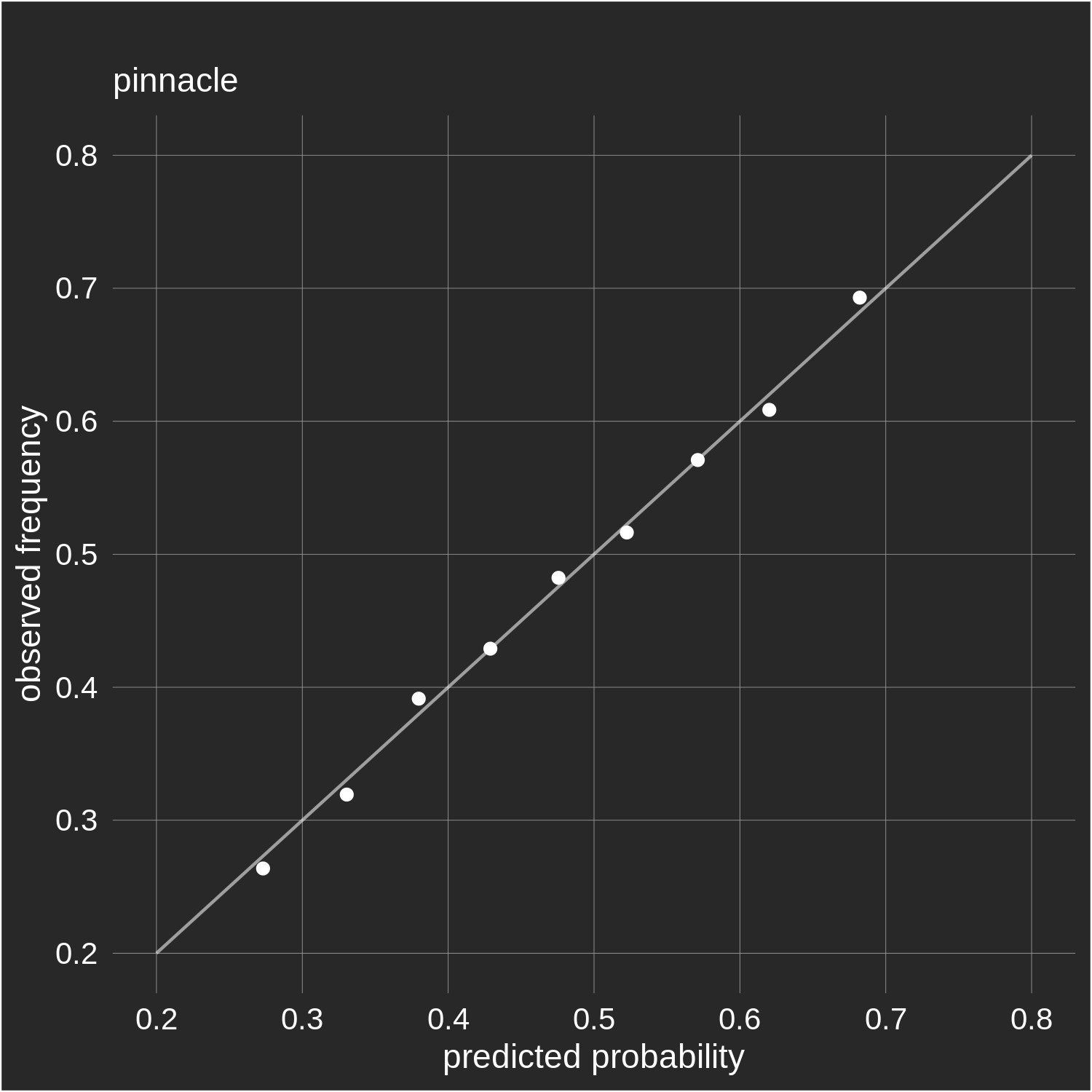
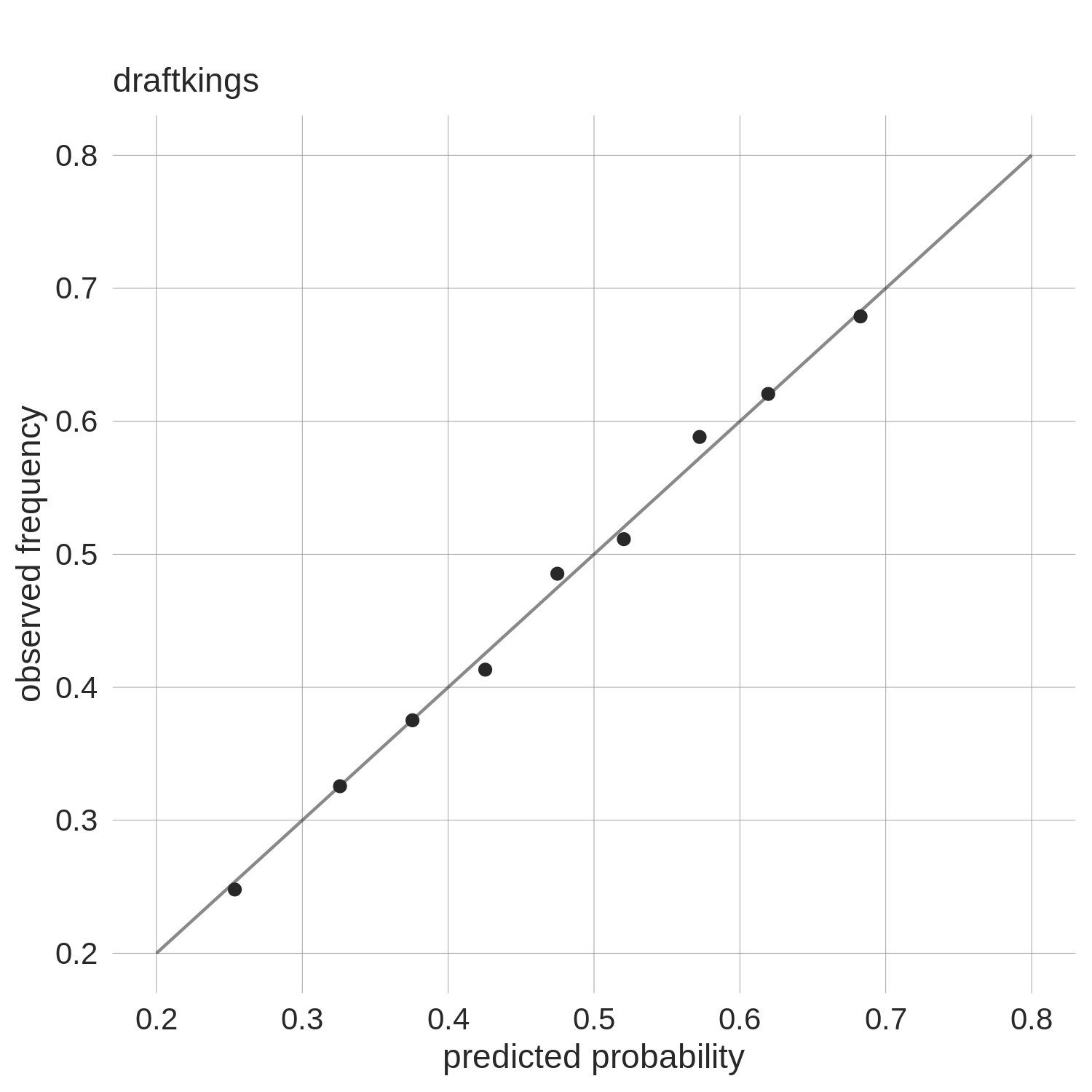
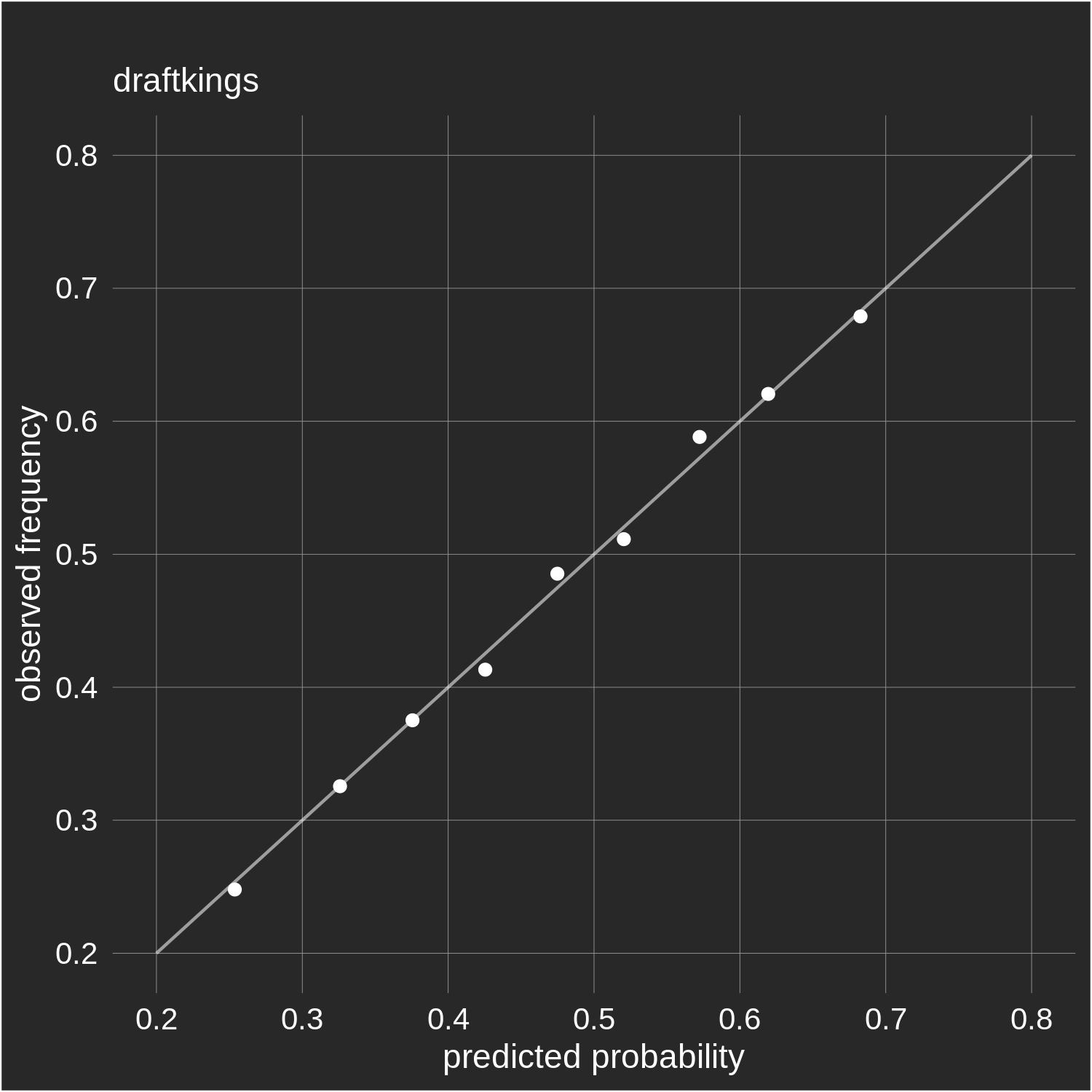
our first and last efforts at scraping them.) Consider the two plots below which show the "calibration" of both Pinnacle and DraftKings'
margin-free closing odds.
Each data point represents a group of predictions. For example,
the point second from the left in the DraftKings plot is
comprised of all golfers with margin-free odds between 30 and 35%; their
mean was 32.6% (value on x-axis) and
this set of golfers ultimately won 32.5% of the time (value on y-axis). The line
in each plot represents perfect calibration (x=y).
Overall, both sets of odds do a good job of approximating actual frequencies: when
DraftKings says a golfer has a 60% chance of winning, they do in fact win about 60% of the time (as evidenced
by the observed win rate of a large number of "60% predictions"). The
same can be said for Pinnacle's odds.
However, calibration plots, used as a means of evaluating the quality of a model,
aren't particularly informative. Any halfway-decent model can
be made to look good on
a plot like this. To see this,
suppose that in the 60% bin the golfers can be evenly divided into a subgroup of golfers that
won 58% of the time and another subgroup that won 62% of the time. If Pinnacle (on average) assigns
to these subgroups of golfers win probabilities of 58% and 62% respectively, while DraftKings (on average) assigns
to golfers in both subgroups win probabilities of 60%, we can definitively say that Pinnacle's model is better. But,
both models will look the same in these calibration plots.
Fortunately a much sharper test of prediction quality can be found by using a bookmaker's odds to bet against other books. That is, we use one book's margin-free probabilities to estimate expected value using other books' offered (i.e. margin-included) odds. For example, consider the 1st Round 3-Ball between Andrew Landry, Jordan Spieth, and Cameron Champ at the 2020 Memorial. DraftKings offered closing odds of 3.25 (or, in American format, +225) on Landry, 2.35 (+135) on Spieth, and 2.8 (+180) on Champ; Bet365 offered respective odds of 3.75 (+275), 2.25 (+125), and 2.62 (+162). To calculate DraftKings' margin-free price for Andrew Landry, we simply divide his implied probability (30.77%) by the sum of all 3 implied probabilities (30.77% + 42.55% + 35.71% = 109.04%), which yields 28.2% (equivalently 3.54 or +254). This margin-free implied probability from DraftKings is then taken as our "true" probability when calculating expected value against Bet365's price; for Landry, this results in an expected value of 5.75%.
Ideally we would perform this exercise book-by-book, but unfortunately the sample sizes simply aren't large enough. Part of the sample size issue stems from the fact that for this exercise we can only use bets that both books offered odds on. The next two tables show the results using Pinnacle and DraftKings' odds, respectively, to place bets at all other books for various levels of expected value. There are many duplicate bets in these tables: for any given bet there might be several books offering it, and, further, both golfers from each bet will be assigned to an expected value bin. Pinnacle's table is based off a total of 10972 unique bets and Draftkings' is based off of 8178 unique bets. We use 1 unit stakes for all bets.
This is bad news for DraftKings and good news for Pinnacle. When Pinnacle says that a bet has
an expected value of 4%, the realized return (averaged over many +4% EV bets) is about 4%.
In Pinnacle's results there is a (roughly)
1 to 1 relationship between expected and actual ROI, while
for DraftKings it is only a slightly positive relationship.
For Pinnacle this means that closing odds from other books add little predictive value to
their closing odds. Given that Pinnacle's odds move the most from opening to close,
this result is not surprising; we would expect that their closing line incorporates all relevant
information. Put differently, if you were to optimally predict matchup results
using the closing odds from all books, the best predictions would be achieved by putting 95-100%
of the weight on Pinnacle. More generally, a simple way to estimate the optimal weighting
between the model odds being used to calculate expected value, and the odds being bet against, is to
see where actual ROI sits in relation to random (or blind) betting returns and expected ROI. For example,
if random returns are -5%, expected returns are 5%, and actual returns were 2%, we would
conclude that the correct weighting is 70% on the model and 30% on the bookmaker (ignoring sample
size issues).
For DraftKings, the slight positive relationship between expected and realized return indicates that their closing line adds a bit of predictive value to the other books' closing lines (perhaps not at Pinnacle, but at other books). If you repeat this exercise using closing lines from the other bookmakers in the first table of this article there are not many noteworthy takeaways. BetOnline, 5Dimes and Bovada tend to just copy Pinnacle (or Bet365, in the case of Bovada) when it's possible. Bet365 and Betcris, along with Pinnacle and DraftKings, appear to be the books that actually provide independent pricing; they don't move their lines as much as Pinnacle so we will defer their detailed discussion to the next section. As the above analysis suggests, the closing lines at Betcris and Bet365 do not add much value to Pinnacle's closing line.
To finish this section, here are the betting results that could be achieved with different expected value thresholds using Pinnacle's closing odds to bet against other books' closing odds (which is a feasible betting strategy). For example, the first row indicates there were a total of 4803 bets with an expected value of at least 0% according to Pinnacle's margin-free closing lines, 3435 of which were unique bets. Placing 1 unit on each of these bets yielded a profit of 88 units and a return of 1.8%. Returns begin to decline at higher thresholds, but sample sizes are also smaller.
Fortunately a much sharper test of prediction quality can be found by using a bookmaker's odds to bet against other books. That is, we use one book's margin-free probabilities to estimate expected value using other books' offered (i.e. margin-included) odds. For example, consider the 1st Round 3-Ball between Andrew Landry, Jordan Spieth, and Cameron Champ at the 2020 Memorial. DraftKings offered closing odds of 3.25 (or, in American format, +225) on Landry, 2.35 (+135) on Spieth, and 2.8 (+180) on Champ; Bet365 offered respective odds of 3.75 (+275), 2.25 (+125), and 2.62 (+162). To calculate DraftKings' margin-free price for Andrew Landry, we simply divide his implied probability (30.77%) by the sum of all 3 implied probabilities (30.77% + 42.55% + 35.71% = 109.04%), which yields 28.2% (equivalently 3.54 or +254). This margin-free implied probability from DraftKings is then taken as our "true" probability when calculating expected value against Bet365's price; for Landry, this results in an expected value of 5.75%.
Ideally we would perform this exercise book-by-book, but unfortunately the sample sizes simply aren't large enough. Part of the sample size issue stems from the fact that for this exercise we can only use bets that both books offered odds on. The next two tables show the results using Pinnacle and DraftKings' odds, respectively, to place bets at all other books for various levels of expected value. There are many duplicate bets in these tables: for any given bet there might be several books offering it, and, further, both golfers from each bet will be assigned to an expected value bin. Pinnacle's table is based off a total of 10972 unique bets and Draftkings' is based off of 8178 unique bets. We use 1 unit stakes for all bets.
Pinnacle
| exp. value bin | # of bets | exp. roi | roi |
|---|---|---|---|
| < -10% | 6848 | -12.6% | -13.9% |
| > -10% & < -8% | 7267 | -8.9% | -9.3% |
| > -8% & < -6% | 13728 | -6.9% | -5.4% |
| > -6% & < -4% | 20161 | -5% | -5.8% |
| > -4% & < -2% | 16520 | -3.1% | -2.5% |
| > -2% & < 0% | 6669 | -1.1% | -3.6% |
| > 0% & < 2% | 2901 | 0.8% | 0.6% |
| > 2% | 1902 | 4.5% | 3.7% |
DraftKings
| exp. value bin | # of bets | exp. roi | roi |
|---|---|---|---|
| < -10% | 13393 | -13.8% | -9.3% |
| > -10% & < -8% | 7818 | -8.9% | -8.5% |
| > -8% & < -6% | 8718 | -7% | -5.7% |
| > -6% & < -4% | 9500 | -5% | -5% |
| > -4% & < -2% | 8263 | -3% | -4% |
| > -2% & < 0% | 6219 | -1.1% | -2.5% |
| > 0% & < 2% | 3834 | 0.9% | -5.3% |
| > 2% | 4989 | 5.6% | -4.1% |
For DraftKings, the slight positive relationship between expected and realized return indicates that their closing line adds a bit of predictive value to the other books' closing lines (perhaps not at Pinnacle, but at other books). If you repeat this exercise using closing lines from the other bookmakers in the first table of this article there are not many noteworthy takeaways. BetOnline, 5Dimes and Bovada tend to just copy Pinnacle (or Bet365, in the case of Bovada) when it's possible. Bet365 and Betcris, along with Pinnacle and DraftKings, appear to be the books that actually provide independent pricing; they don't move their lines as much as Pinnacle so we will defer their detailed discussion to the next section. As the above analysis suggests, the closing lines at Betcris and Bet365 do not add much value to Pinnacle's closing line.
To finish this section, here are the betting results that could be achieved with different expected value thresholds using Pinnacle's closing odds to bet against other books' closing odds (which is a feasible betting strategy). For example, the first row indicates there were a total of 4803 bets with an expected value of at least 0% according to Pinnacle's margin-free closing lines, 3435 of which were unique bets. Placing 1 unit on each of these bets yielded a profit of 88 units and a return of 1.8%. Returns begin to decline at higher thresholds, but sample sizes are also smaller.
| threshold | # of bets | uniques | exp. roi | profit | roi |
|---|---|---|---|---|---|
| 0% | 4803 | 3435 | 2.28% | 88.4 | 1.84% |
| 1% | 3040 | 2332 | 3.34% | 93.3 | 3.07% |
| 2% | 1902 | 1532 | 4.47% | 71.3 | 3.75% |
| 3% | 1140 | 955 | 5.82% | 23.1 | 2.03% |
| 4% | 743 | 633 | 7.07% | 8.1 | 1.08% |
| 5% | 511 | 446 | 8.25% | -3.0 | -0.59% |
Before you close, you have to open
Pinnacle's closing lines are accurate because they move in response
to useful information revealing itself in the market. Next we look at how
other bookmakers' opening odds influence Pinnacle's odds movement from open to close. Of course
with this exercise I'm not suggesting that Pinnacle is directly responding to other bookmakers'
odds — I have no idea how their odds are set — but there are many indirect ways
bookmakers' odds could affect one another.
To start let's focus on Betcris and Pinnacle. Since we started tracking Betcris' odds in late 2019, we have 3492 bets that were offered by both bookmakers. Of those 3492 bets, there were 314 instances where we only scraped odds at one point in time for at least one of the books; that is, the opening and closing odds were the same. We drop these bets for this analysis, leaving us with a sample size of 3178. (This typically occurs either due to errors in our scraping scripts or odds that are posted without much time before the golfers started.) Because Pinnacle and Betcris apply differential margins to their odds, it will be easiest to focus on the margin-free probabilities for this exercise. Consider the 3rd Round Matchup between Christiaan Bezuidenhout and Sam Burns at the 2020 Arnold Palmer Invitational: Betcris' opening margin-free price for Bezuidenhout was 46.6% while Pinnacle's was 60.5%. Thus Pinnacle's opening price was 29.8% (\( \frac{60.5}{46.6} - 1 \)) higher than Betcris'. The closing margin-free price for Betcris was 49.2% while at Pinnacle it was 50.1%. Therefore Betcris' price, from opening to close, moved 18.9% of the way towards Pinnacle's opening price; Pinnacle's price, from opening to close, moved 74.5% of the way towards Betcris' opening price.
We repeat this calculation for all 3178 bets, focusing only on the odds offered for the first listed player in each matchup to avoid double counting. There were 1401 instances where one of Pinnacle or Betcris showed an advantage of at least 5% (the "advantage" in our example above was 29.8%). In these bets, Pinnacle's price on average moved 54.7% of the way to Betcris' opening probability, while Betcris on average moved just 15.6% of the way to Pinnacle's opener. Performing the same exercise except only with bets where there is a 10% advantage, we have a sample of 464 bets, and respective average moves of 62.3% and 15.0% for Pinnacle and Betcris. Moving the cutoff to 15%, there are 146 bets and average moves of 70.2% and 12.6% for Pinnacle and Betcris. Among other things, these movements can tell us about "closing line value": if you start with a 5% advantage against a book's opening odds, and the closing odds move 50% of the distance towards your model's odds, then closing line value would be 2.5% (using a book's margin-free odds).
An important caveat here is that for 72-hole matches (which constitute ~70% of this sample), Pinnacle posts their opening odds before Betcris. Therefore part of Pinnacle's price movement towards Betcris could be occurring before Betcris actually posts their odds [3]. In any case, the takeaway here is that Pinnacle's closing prices are influenced by Betcris' prices to a considerable degree. Also, given that in the previous section we argued that Pinnacle's closing lines are the most accurate in our database, Betcris' closing prices should move towards Pinnacle's more than they currently do (if their only concern when setting odds was accuracy, which it likely is not) [4]. The next table summarizes the results of this exercise for other pairs of books. Also included in this table is the correlation between the opening odds, and closing odds, of the relevant pair (for Bet365/DK we exclude 3-balls in the correlation to make it more comparable to the other pairs of books).
A minor point on the correlations is that each pair of books
covers a different sample of bets, and therefore some samples may yield naturally higher or lower
correlations. When the opening odds of
DraftKings (or Bet365) have large discrepancies with Pinnacle, both
books show some movement towards each other by closing.
Given that Pinnacle's closing lines are pretty accurate,
this tell us two things: 1) opening lines at Bet365 and DraftKings add some value
to Pinnacle's opening lines, and 2) opening lines at Bet365 and DraftKings should be
moving a lot more than they do (which should surprise nobody). Paradoxically, the
correlation between DraftKings and Pinnacle's closing odds actually declines
slightly relative to the correlation between their opening odds; this is possible because
Pinnacle's lines move a lot while DraftKings' do not [5].
We observe the same phenomenon with Bet365/Pinnacle.
When I do this analysis for, e.g., 5Dimes vs. Pinnacle, the timing issue becomes apparent: I find that Pinnacle's lines move a lot towards 5Dimes' opening odds (>50%). This is largely driven by the fact that 5Dimes often follows Pinnacle's odds closely (correlation 0.975 between their opening odds), and as a consequence posts their opening odds after Pinnacle. If Pinnacle's odds have already moved before we scrape 5Dimes' opening odds (which mimic Pinnacle's prices at the time), it will give us the impression that Pinnacle's odds "moved towards" 5Dimes' openers.
The previous table is basically sufficient for understanding the quality of the opening lines at these 4 books. If we agree that Pinnacle's closing line is accurate, and combine that with the observation that Pinnacle's movement from opening to closing is influenced by Betcris to a large degree, we would conclude that Betcris' opening lines are adding a lot of predictive value to Pinnacle's opening lines. By the same logic, the openers at DraftKings and Bet365 also add some value to Pinnacle's openers. Finally, we can also say that Pinnacle's opening lines themselves are providing a reasonable amount of predictive value, as evidenced by the fact that they only move 50-70% of the way to Betcris' opening odds (depending on the starting discrepancy). Given that Betcris moves Pinnacle's opening lines more than 50% of the way towards their opening lines, we would expect their openers to be the most accurate. If we did not want to rely on the assumption of the accuracy of Pinnacle's closing line to compare opening line quality, we could repeat the exercise from the previous section and use each book's opening odds to bet against other books' opening odds. However the sample sizes just aren't large enough to draw very sharp conclusions (for example, there are only ~1000 bets that Betcris and Bet365 both offered odds on). Without providing specifics, the main takeaways from the exercise were that Pinnacle and Betcris have opening lines that are a step above DraftKings and Bet365 in terms of accuracy, but also that all 4 books' opening lines add some degree of predictive value to each other.
We'll finish this section as we did the last: the next table shows the betting results using Pinnacle's opening lines to bet against all other books' openers (which is a feasible strategy given Pinnacle almost always opens first). As mentioned earlier, keep in mind that these might not literally be Pinnacle's opening odds (but should always be from within an hour or two of opening).
A blind betting strategy returns about -5.5% on this sample of bets,
which means that Pinnacle's realized ROI sits just over halfway
between random and expected returns. At the higher thresholds this relationship seems to break down a bit,
but there are some serious sample size issues. Another point about sample size to consider here (and throughout
this article) is that some bets are correlated: for example, a bookmaker might offer 5 tournament matchups
involving the same golfer, which decreases the effective sample size.
To start let's focus on Betcris and Pinnacle. Since we started tracking Betcris' odds in late 2019, we have 3492 bets that were offered by both bookmakers. Of those 3492 bets, there were 314 instances where we only scraped odds at one point in time for at least one of the books; that is, the opening and closing odds were the same. We drop these bets for this analysis, leaving us with a sample size of 3178. (This typically occurs either due to errors in our scraping scripts or odds that are posted without much time before the golfers started.) Because Pinnacle and Betcris apply differential margins to their odds, it will be easiest to focus on the margin-free probabilities for this exercise. Consider the 3rd Round Matchup between Christiaan Bezuidenhout and Sam Burns at the 2020 Arnold Palmer Invitational: Betcris' opening margin-free price for Bezuidenhout was 46.6% while Pinnacle's was 60.5%. Thus Pinnacle's opening price was 29.8% (\( \frac{60.5}{46.6} - 1 \)) higher than Betcris'. The closing margin-free price for Betcris was 49.2% while at Pinnacle it was 50.1%. Therefore Betcris' price, from opening to close, moved 18.9% of the way towards Pinnacle's opening price; Pinnacle's price, from opening to close, moved 74.5% of the way towards Betcris' opening price.
We repeat this calculation for all 3178 bets, focusing only on the odds offered for the first listed player in each matchup to avoid double counting. There were 1401 instances where one of Pinnacle or Betcris showed an advantage of at least 5% (the "advantage" in our example above was 29.8%). In these bets, Pinnacle's price on average moved 54.7% of the way to Betcris' opening probability, while Betcris on average moved just 15.6% of the way to Pinnacle's opener. Performing the same exercise except only with bets where there is a 10% advantage, we have a sample of 464 bets, and respective average moves of 62.3% and 15.0% for Pinnacle and Betcris. Moving the cutoff to 15%, there are 146 bets and average moves of 70.2% and 12.6% for Pinnacle and Betcris. Among other things, these movements can tell us about "closing line value": if you start with a 5% advantage against a book's opening odds, and the closing odds move 50% of the distance towards your model's odds, then closing line value would be 2.5% (using a book's margin-free odds).
An important caveat here is that for 72-hole matches (which constitute ~70% of this sample), Pinnacle posts their opening odds before Betcris. Therefore part of Pinnacle's price movement towards Betcris could be occurring before Betcris actually posts their odds [3]. In any case, the takeaway here is that Pinnacle's closing prices are influenced by Betcris' prices to a considerable degree. Also, given that in the previous section we argued that Pinnacle's closing lines are the most accurate in our database, Betcris' closing prices should move towards Pinnacle's more than they currently do (if their only concern when setting odds was accuracy, which it likely is not) [4]. The next table summarizes the results of this exercise for other pairs of books. Also included in this table is the correlation between the opening odds, and closing odds, of the relevant pair (for Bet365/DK we exclude 3-balls in the correlation to make it more comparable to the other pairs of books).
| book1 | book2 |
correlation b/w opening odds |
correlation b/w closing odds |
full sample size | advantage threshold |
# of bets | book1 -> book2 | book2 -> book1 |
|---|---|---|---|---|---|---|---|---|
| bet365 | pinnacle | 0.94 | 0.94 | 2480 | 5% | 777 | 8.1% | 8.7% |
| bet365 | pinnacle | 0.94 | 0.94 | 2480 | 15% | 85 | 10.3% | 14.8% |
| bet365 | betcris | 0.82 | 0.85 | 836 | 5% | 384 | 4.6% | 12.5% |
| bet365 | betcris | 0.82 | 0.85 | 836 | 15% | 65 | 11.0% | 11.5% |
| bet365 | draftkings | 0.91* | 0.94* | 3925 | 5% | 1926 | 5.6% | 6.6% |
| bet365 | draftkings | 0.91* | 0.94* | 3925 | 15% | 368 | 8.8% | 10.5% |
| draftkings | pinnacle | 0.94 | 0.94 | 4088 | 5% | 1258 | 9.7% | 21.8% |
| draftkings | pinnacle | 0.94 | 0.94 | 4088 | 15% | 58 | 18.4% | 25.0% |
| draftkings | betcris | 0.86 | 0.89 | 1022 | 5% | 460 | 6.5% | 13.4% |
| draftkings | betcris | 0.86 | 0.89 | 1022 | 15% | 55 | 17.3% | 15.6% |
| betcris | pinnacle | 0.83 | 0.95 | 3178 | 5% | 1401 | 15.6% | 54.7% |
| betcris | pinnacle | 0.83 | 0.95 | 3178 | 15% | 146 | 12.6% | 70.2% |
When I do this analysis for, e.g., 5Dimes vs. Pinnacle, the timing issue becomes apparent: I find that Pinnacle's lines move a lot towards 5Dimes' opening odds (>50%). This is largely driven by the fact that 5Dimes often follows Pinnacle's odds closely (correlation 0.975 between their opening odds), and as a consequence posts their opening odds after Pinnacle. If Pinnacle's odds have already moved before we scrape 5Dimes' opening odds (which mimic Pinnacle's prices at the time), it will give us the impression that Pinnacle's odds "moved towards" 5Dimes' openers.
The previous table is basically sufficient for understanding the quality of the opening lines at these 4 books. If we agree that Pinnacle's closing line is accurate, and combine that with the observation that Pinnacle's movement from opening to closing is influenced by Betcris to a large degree, we would conclude that Betcris' opening lines are adding a lot of predictive value to Pinnacle's opening lines. By the same logic, the openers at DraftKings and Bet365 also add some value to Pinnacle's openers. Finally, we can also say that Pinnacle's opening lines themselves are providing a reasonable amount of predictive value, as evidenced by the fact that they only move 50-70% of the way to Betcris' opening odds (depending on the starting discrepancy). Given that Betcris moves Pinnacle's opening lines more than 50% of the way towards their opening lines, we would expect their openers to be the most accurate. If we did not want to rely on the assumption of the accuracy of Pinnacle's closing line to compare opening line quality, we could repeat the exercise from the previous section and use each book's opening odds to bet against other books' opening odds. However the sample sizes just aren't large enough to draw very sharp conclusions (for example, there are only ~1000 bets that Betcris and Bet365 both offered odds on). Without providing specifics, the main takeaways from the exercise were that Pinnacle and Betcris have opening lines that are a step above DraftKings and Bet365 in terms of accuracy, but also that all 4 books' opening lines add some degree of predictive value to each other.
We'll finish this section as we did the last: the next table shows the betting results using Pinnacle's opening lines to bet against all other books' openers (which is a feasible strategy given Pinnacle almost always opens first). As mentioned earlier, keep in mind that these might not literally be Pinnacle's opening odds (but should always be from within an hour or two of opening).
| threshold | # of bets | uniques | exp. roi | profit | roi |
|---|---|---|---|---|---|
| 0% | 6098 | 3996 | 3.36% | -66.7 | -1.09% |
| 1% | 4486 | 3122 | 4.41% | 13.3 | 0.30% |
| 2% | 3259 | 2382 | 5.52% | 4.4 | 0.13% |
| 3% | 2294 | 1725 | 6.80% | 11.6 | 0.50% |
| 4% | 1651 | 1272 | 8.09% | 10.5 | 0.64% |
| 5% | 1227 | 955 | 9.35% | 15.8 | 1.29% |
| 6% | 948 | 755 | 10.49% | 16.4 | 1.73% |
| 7% | 720 | 572 | 11.77% | -14.1 | -1.96% |
| 8% | 568 | 448 | 12.93% | -14.7 | -2.59% |
| 9% | 429 | 339 | 14.39% | -8.3 | -1.94% |
| 10% | 338 | 270 | 15.71% | 10.6 | 3.13% |
How good is the Data Golf model?
If a bettor can add predictive value
to the bookmaker's odds in any way
they stand a chance of making money;
at the very least
they will not lose as much money as they would if betting randomly.
A successful bettor does not require a model that fits
the data better than the bookmaker's odds, but rather just one
that can improve upon those odds enough to overcome the margin
they are up against.
In comparing our model's odds to those of bookmakers, I've developed a greater appreciation for the quality of their predictions. Even a "soft" book like Bet365 has margin-free probabilities that fit the data pretty well; since 2019, their matchup odds have performed similar to ours. That is, while we can make money betting against Bet365 (evidence to come), they could also make money betting against us (if we added some reasonable margin to our odds and started bookmaking). As alluded to in the previous paragraph, if you have a model that fits the data as well as the model you are betting against (e.g. suppose a 50-50 weighting of the two sets of odds is optimal) you are likely in a very good position. Even if the optimal weighting puts only 15-30% on your model, that can be sufficient depending on the margin and the size of the discrepancies between your model and the offered odds.
Let's take a detailed look at how the Data Golf model performed over the last 2 years. Recall that in 2019 our model did not include course-specific adjustments, while in 2020 our PGA Tour model incorporated both course fit and course history adjustments and our European Tour model incorporated course history. The table below shows our overall betting performance across all books since early 2019 for various expected value thresholds (as before, using a 1-unit stake for all bets). Betting with a 2% threshold means that any bet with an expected value of at least 2% is taken.
A couple points to note. First, blind betting returns averaged across all books
was -5.9%. When evaluating
your betting results this is the benchmark you should compare your performance to;
against a 6% margin, breaking even is actually very good. Second, along with
the number of bets made we also display the number of unique bets
made; if
multiple books are offering the same bet it's likely we will have placed a bet on both
in this exercise.
Betting 1 unit on every positive "edge" according to our model since 2019 results in a cool loss of 420 units. However, with 45866 bets made, this yields a respectable ROI of -0.9%. Given the blind betting strategy returned -5.9%, it's clear we are adding some value to the odds we are betting against. To turn a meaningful profit with our model, an expected value threshold of 5% or higher is required, with profits peaking at the 8% threshold. The fact that ROI stops increasing at the highest expected value thresholds is not too worriesome given the smaller sample sizes (another reminder that 1000 bets is in fact a small sample). Overall, our actual ROI sits slightly under halfway between random betting returns and expected returns, which means that the optimal weighting of our model and the bookmakers is about 45-55 [6]. If our model added no predictive value, actual returns should equal the blind betting return, while if bookmaker odds added no value to our model actual returns should equal expected returns.
Here are two further ways to breakdown these results. First, focusing on the 8% threshold, which is where profits were maximized, the breakdown across bet types was: 72-hole matchups — 2191 bets; 2.1 units profit; 0.1% ROI, 1-round matchups — 3370 bets; 58.2 units profit; 1.7% ROI, and 3-balls — 3542 bets; 342.6 units profit; 9.7% ROI. Second, the table below displays the model's performance by bookmaker using the 8% threshold:
In our published betting results from 2019
and 2020, our average return on matchups and 3-balls
was about 0.9%. All bets were placed through Bet365 and instead of level staking we were using a version
of the Kelly Criterion.
In 2019 the EV thresholds used were probably closer to 5%, while halfway through 2020
we switched to higher thresholds (6-7% for matchups; 8-9% for 3-balls). Given the returns from Bet365 in
this analysis I can't help but feel we got a bit unlucky with our actual betting results.
Next I restrict our sample of possible bets to the 2020 PGA Tour season, which used the most complete version of our model [7].
Now betting every "edge" from our model would have turned a profit.
This is a useful demonstration of the fine line between betting successfully and unsuccessfully.
In our full betting results, optimal predictions put about 45% of the weight on our model's prediction and
55% on the bookmaker's; restricting
to only 2020 PGA Tour predictions the weight on our model increases to 60-65%. This increase was enough
to flip our ROI from -1% to +1%, which is the difference
between seeing your bankroll dwindled down to nothing and seeing it double or triple in size.
The reality is that the models that led to these two ROIs are not very different; thousands of bets
are required to establish a statistically meaningful difference.
Profits in the 2020 PGA Tour season were maximized at the 7% threshold; the profit breakdown by bet type was: 72-hole matchups — 653 bets; +38.7 units; 5.9% ROI, 1-round matchups — 1362 bets; +70.0 profit; 7.8% ROI, and 3-balls — 1740 bets; 237.0 profit; 13.6% ROI. Beyond the 5% threshold sample sizes are pretty small, and it looks like we got lucky in the 7-13% range where actual ROI is approaching expected ROI.
Finally, this last table shows how each book's margin-free odds moved from opening to close in relation to our model's probabilities (using the full time period, but excluding 3-balls). The correlations shown here, as before, might be a bit misleading as the samples they cover are different. For example, the correlation between DG probabilities and Bet365 margin-free probabilities is 0.86 in the Pinnacle-Bet365 overlap sample. This difference likely reflects the fact that those matchups were between more unevenly-matched golfers, which naturally produces stronger correlations. As before, matchups where we only managed to scrape odds at a single point in time are dropped. As an example for clarity's sake, the last 2 columns of the first row indicate the following: there were 874 matchup bets at Bet365 where the opening margin-free odds disagreed with our model's odds by at least 15% (that is, the ratio of our odds to Bet365, or the ratio of Bet365's odds to ours, was at least 1.15); on average in those 874 matchups, Bet365's closing odds moved 5.3% of the distance towards our model's odds.
To conclude this section, here are a few takeaways. First, from our betting performance it's clear
that 3-balls have the weakest odds-setting of the bet
types we considered; this is at least in part because they are only offered
by "softer" bookmakers. Second, matchup odds in golf are solid, regardless of the bookmaker you are considering.
I am skeptical that there are many independent (that is, not incorporating market
prices in some way) matchup models out there
that fit the data better than most bookmakers' odds do. With the high margins
(4-6%) typically built into matchup prices, it is therefore not an easy task to be profitable.
In our case, it was disheartening at first to see that most bookmakers' prices
predict matchup results as well as, or better than, our model does.
There is clearly information that bookmakers are incorporating into
their opening odds that our model is not (and vice versa). As this final section showed however,
it is not necessary to have a perfect model to be successful betting.
A model whose purpose is to generate a profitable betting strategy,
versus one whose purpose is to set odds for bettors to bet against, will be quite different
in how they are best built. One key difference between our model and a bookmaker's margin-free odds
is that we generate more extreme predictions (i.e. closer to 0% or 100%); this doesn't really
hurt you when betting (provided you use a sensible staking strategy) but it could
be very detrimental to a bookmaker. A final takeaway is that our 2020 PGA Tour model
performed very well; hopefully with some improvements in the off-season we can maintain or
increase that advantage.
In comparing our model's odds to those of bookmakers, I've developed a greater appreciation for the quality of their predictions. Even a "soft" book like Bet365 has margin-free probabilities that fit the data pretty well; since 2019, their matchup odds have performed similar to ours. That is, while we can make money betting against Bet365 (evidence to come), they could also make money betting against us (if we added some reasonable margin to our odds and started bookmaking). As alluded to in the previous paragraph, if you have a model that fits the data as well as the model you are betting against (e.g. suppose a 50-50 weighting of the two sets of odds is optimal) you are likely in a very good position. Even if the optimal weighting puts only 15-30% on your model, that can be sufficient depending on the margin and the size of the discrepancies between your model and the offered odds.
Let's take a detailed look at how the Data Golf model performed over the last 2 years. Recall that in 2019 our model did not include course-specific adjustments, while in 2020 our PGA Tour model incorporated both course fit and course history adjustments and our European Tour model incorporated course history. The table below shows our overall betting performance across all books since early 2019 for various expected value thresholds (as before, using a 1-unit stake for all bets). Betting with a 2% threshold means that any bet with an expected value of at least 2% is taken.
| threshold | # of bets | uniques | exp. roi | profit | roi |
|---|---|---|---|---|---|
| 0% | 45866 | 22846 | 5.16% | -420.0 | -0.92% |
| 1% | 37610 | 19348 | 6.19% | -137.5 | -0.37% |
| 2% | 30702 | 16303 | 7.25% | -86.1 | -0.28% |
| 3% | 24832 | 13523 | 8.37% | -31.2 | -0.13% |
| 4% | 20136 | 11203 | 9.51% | 79.7 | 0.40% |
| 5% | 16420 | 9302 | 10.65% | 237.5 | 1.45% |
| 6% | 13463 | 7731 | 11.79% | 279.1 | 2.07% |
| 7% | 11045 | 6489 | 12.95% | 379.0 | 3.43% |
| 8% | 9103 | 5435 | 14.12% | 402.9 | 4.43% |
| 9% | 7468 | 4478 | 15.35% | 359.0 | 4.81% |
| 10% | 6155 | 3730 | 16.60% | 274.4 | 4.46% |
| 11% | 5174 | 3181 | 17.76% | 202.4 | 3.91% |
| 12% | 4352 | 2700 | 18.94% | 226.3 | 5.20% |
| 13% | 3697 | 2304 | 20.09% | 212.5 | 5.75% |
| 14% | 3121 | 1955 | 21.31% | 190.8 | 6.11% |
| 15% | 2630 | 1638 | 22.58% | 225.6 | 8.58% |
| 16% | 2241 | 1410 | 23.81% | 201.8 | 9.00% |
| 17% | 1928 | 1227 | 25.00% | 173.2 | 8.98% |
| 18% | 1661 | 1060 | 26.21% | 145.2 | 8.74% |
| 19% | 1433 | 921 | 27.44% | 113.8 | 7.94% |
| 20% | 1242 | 796 | 28.67% | 83.6 | 6.73% |
Betting 1 unit on every positive "edge" according to our model since 2019 results in a cool loss of 420 units. However, with 45866 bets made, this yields a respectable ROI of -0.9%. Given the blind betting strategy returned -5.9%, it's clear we are adding some value to the odds we are betting against. To turn a meaningful profit with our model, an expected value threshold of 5% or higher is required, with profits peaking at the 8% threshold. The fact that ROI stops increasing at the highest expected value thresholds is not too worriesome given the smaller sample sizes (another reminder that 1000 bets is in fact a small sample). Overall, our actual ROI sits slightly under halfway between random betting returns and expected returns, which means that the optimal weighting of our model and the bookmakers is about 45-55 [6]. If our model added no predictive value, actual returns should equal the blind betting return, while if bookmaker odds added no value to our model actual returns should equal expected returns.
Here are two further ways to breakdown these results. First, focusing on the 8% threshold, which is where profits were maximized, the breakdown across bet types was: 72-hole matchups — 2191 bets; 2.1 units profit; 0.1% ROI, 1-round matchups — 3370 bets; 58.2 units profit; 1.7% ROI, and 3-balls — 3542 bets; 342.6 units profit; 9.7% ROI. Second, the table below displays the model's performance by bookmaker using the 8% threshold:
| book | # of bets | exp. roi | profit | roi |
|---|---|---|---|---|
| bovada | 1998 | 14.99% | 147.3 | 7.37% |
| bet365 | 2240 | 15.11% | 106.6 | 4.76% |
| willhill | 335 | 14.62% | 50.2 | 15.00% |
| unibet | 184 | 16.68% | 41.0 | 22.3% |
| betonline | 185 | 12.07% | 21.1 | 11.43% |
| 5dimes | 1254 | 12.88% | 16.1 | 1.28% |
| fanduel | 218 | 14.93% | 14.2 | 6.51% |
| pinnacle | 1040 | 12.78% | 13.0 | 1.25% |
| betcris | 324 | 11.91% | 0.1 | 0.03% |
| sportsbook | 321 | 13.26% | -1.5 | -0.45% |
| draftkings | 1004 | 13.65% | -5.3 | -0.52% |
Next I restrict our sample of possible bets to the 2020 PGA Tour season, which used the most complete version of our model [7].
| threshold | # of bets | uniques | exp. roi | profit | roi |
|---|---|---|---|---|---|
| 0% | 17420 | 8212 | 4.82% | 163.6 | 0.94% |
| 1% | 14043 | 6884 | 5.86% | 279.5 | 1.99% |
| 2% | 11228 | 5755 | 6.96% | 249.3 | 2.22% |
| 3% | 8896 | 4715 | 8.13% | 270.6 | 3.04% |
| 4% | 7144 | 3897 | 9.27% | 344.7 | 4.82% |
| 5% | 5665 | 3156 | 10.53% | 327.7 | 5.79% |
| 6% | 4632 | 2628 | 11.66% | 331.0 | 7.15% |
| 7% | 3755 | 2175 | 12.87% | 345.7 | 9.21% |
| 8% | 3090 | 1828 | 14.03% | 334.3 | 10.82% |
| 9% | 2554 | 1505 | 15.19% | 326.7 | 12.79% |
| 10% | 2096 | 1248 | 16.43% | 271.5 | 12.95% |
| 11% | 1777 | 1068 | 17.5% | 237.5 | 13.36% |
| 12% | 1497 | 907 | 18.62% | 231.2 | 15.45% |
| 13% | 1267 | 781 | 19.74% | 183.1 | 14.45% |
| 14% | 1053 | 659 | 21.01% | 129.1 | 12.26% |
| 15% | 880 | 557 | 22.3% | 133.5 | 15.17% |
| 16% | 754 | 475 | 23.44% | 123.8 | 16.42% |
| 17% | 654 | 412 | 24.5% | 94.0 | 14.37% |
| 18% | 567 | 361 | 25.59% | 84.1 | 14.84% |
| 19% | 485 | 312 | 26.79% | 64.6 | 13.31% |
| 20% | 420 | 270 | 27.92% | 46.4 | 11.05% |
Profits in the 2020 PGA Tour season were maximized at the 7% threshold; the profit breakdown by bet type was: 72-hole matchups — 653 bets; +38.7 units; 5.9% ROI, 1-round matchups — 1362 bets; +70.0 profit; 7.8% ROI, and 3-balls — 1740 bets; 237.0 profit; 13.6% ROI. Beyond the 5% threshold sample sizes are pretty small, and it looks like we got lucky in the 7-13% range where actual ROI is approaching expected ROI.
Finally, this last table shows how each book's margin-free odds moved from opening to close in relation to our model's probabilities (using the full time period, but excluding 3-balls). The correlations shown here, as before, might be a bit misleading as the samples they cover are different. For example, the correlation between DG probabilities and Bet365 margin-free probabilities is 0.86 in the Pinnacle-Bet365 overlap sample. This difference likely reflects the fact that those matchups were between more unevenly-matched golfers, which naturally produces stronger correlations. As before, matchups where we only managed to scrape odds at a single point in time are dropped. As an example for clarity's sake, the last 2 columns of the first row indicate the following: there were 874 matchup bets at Bet365 where the opening margin-free odds disagreed with our model's odds by at least 15% (that is, the ratio of our odds to Bet365, or the ratio of Bet365's odds to ours, was at least 1.15); on average in those 874 matchups, Bet365's closing odds moved 5.3% of the distance towards our model's odds.
| book | correlation w/ opening odds |
correlation w/ closing odds |
sample size (>5% adv.) |
book -> dg (>5% adv.) |
sample size (>15% adv.) |
book -> dg (>15% adv.) |
|---|---|---|---|---|---|---|
| bet365 | 0.74 | 0.76 | 4285 | 3.0% | 874 | 5.3% |
| betcris | 0.81 | 0.82 | 3464 | 10.0% | 451 | 11.8% |
| draftkings | 0.86 | 0.87 | 4081 | 3.4% | 697 | 5.7% |
| pinnacle | 0.87 | 0.90 | 5269 | 26.2% | 797 | 30.0% |