Analytics Blog
Analytics Blog
November 25, 2021
Who benefits from wide fairways?
— Analyzing the impact of hole characteristics on the performance of specific players
An interesting idea put forward in certain parts of golf punditry is that wider fairways actually
benefit short and accurate golfers, while
narrow fairways (and long rough) benefit long and inaccurate golfers. The intuition given for this is typically
twofold: first, accurate golfers can't realize their advantage if everyone is hitting from the rough, and
second, it's a bigger disadvantage to lose distance to the field in the rough than the fairway.
This is a counterintuitive claim
that hasn't received the scrunity it deserves.
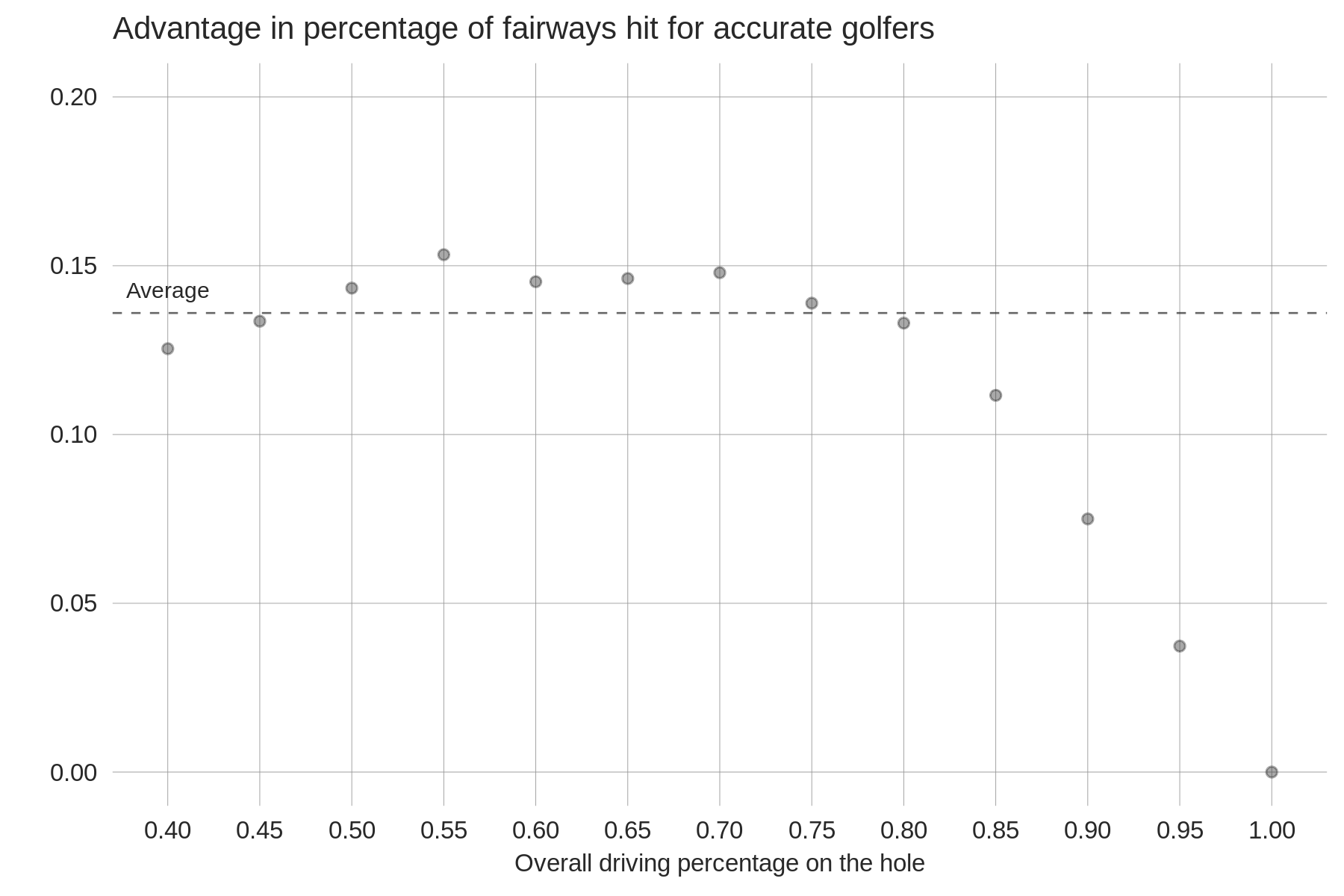
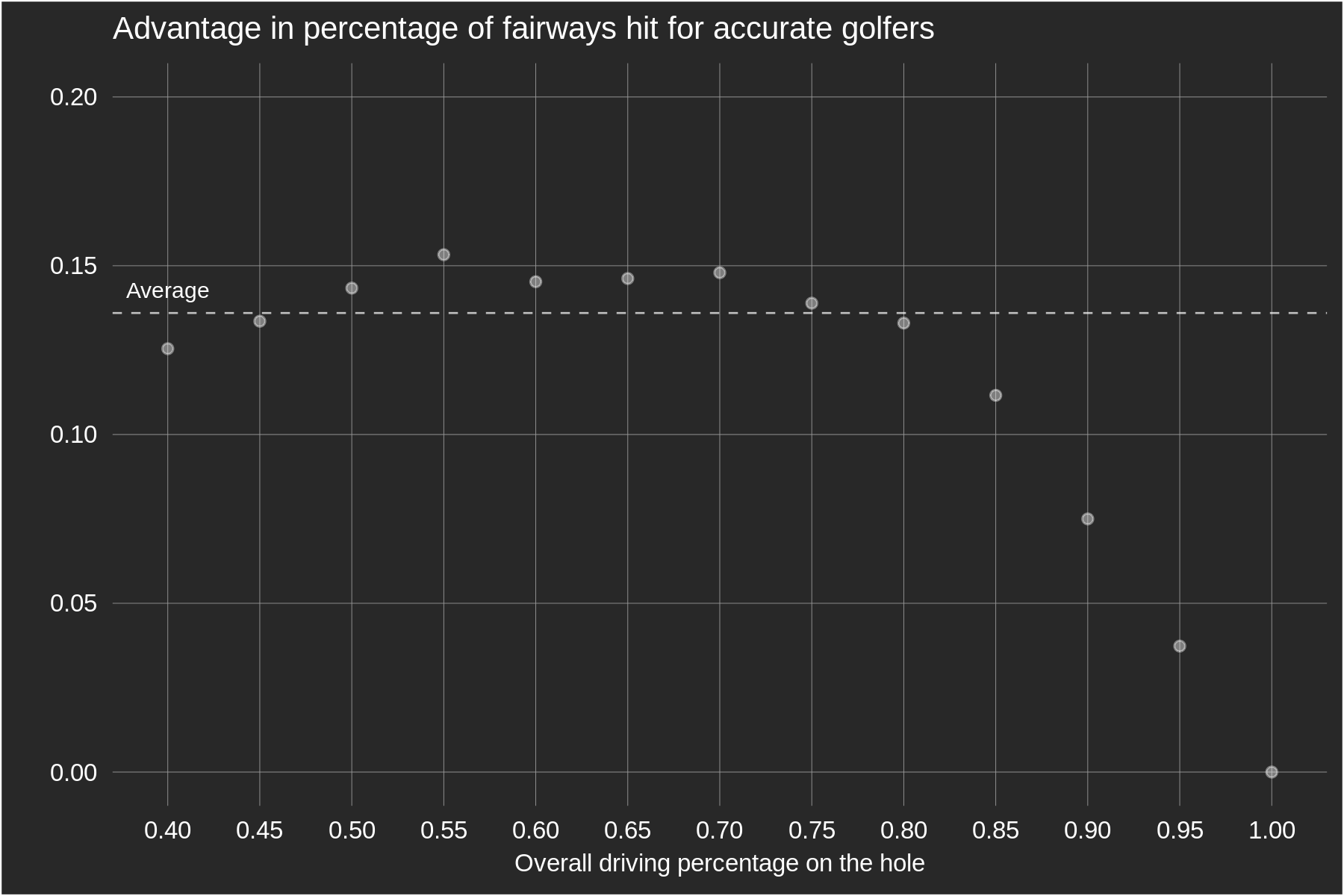
The plot below uses PGA Tour data from 2019-2021 for non-par 3 holes to estimate the driving accuracy difference between accurate and inaccurate golfers as a function of the overall driving accuracy percentage of the hole (we'll use this instead of fairway width, as the conditions of the course — e.g. firmness — can change the "effective" fairway width). Holes are grouped into bins at 5% intervals (e.g. the value at 55% uses holes with a DA % between 52.5% and 57.5%), and accurate golfers are defined to be those at least 1 standard deviation above average in our measure of driving accuracy skill, while inaccurate golfers are at least 1 standard deviation below average in that measure.
The "average" line indicates that across all PGA Tour holes, accurate drivers have a DA % that is 13.6 percentage points higher than inaccurate drivers (73.2% to 59.6% — note that we are counting balls in the intermediate rough as a fairway hit). The data point at 55% tells us that on holes where the field's driving accuracy was between 52.5% and 57.5%, accurate drivers were slightly more than 15 percentage points more likely to hit the fairway than inaccurate drivers. Only 1.5% of holes had an overall driving accuracy percentage below 40%, so they are all placed in the 40% bin. For holes with driving accuracy percentages between 50% and 80%, which characterizes 80% of holes on the PGA Tour, the driving accuracy advantage for accurate players is roughly constant at 13-15%. For holes with a DA % above 0.85 (6% of all holes) this advantage declines sharply; it's likely that a similar decline would be observed for holes below 0.40 DA %, but there simply aren't many PGA Tour holes in that range.
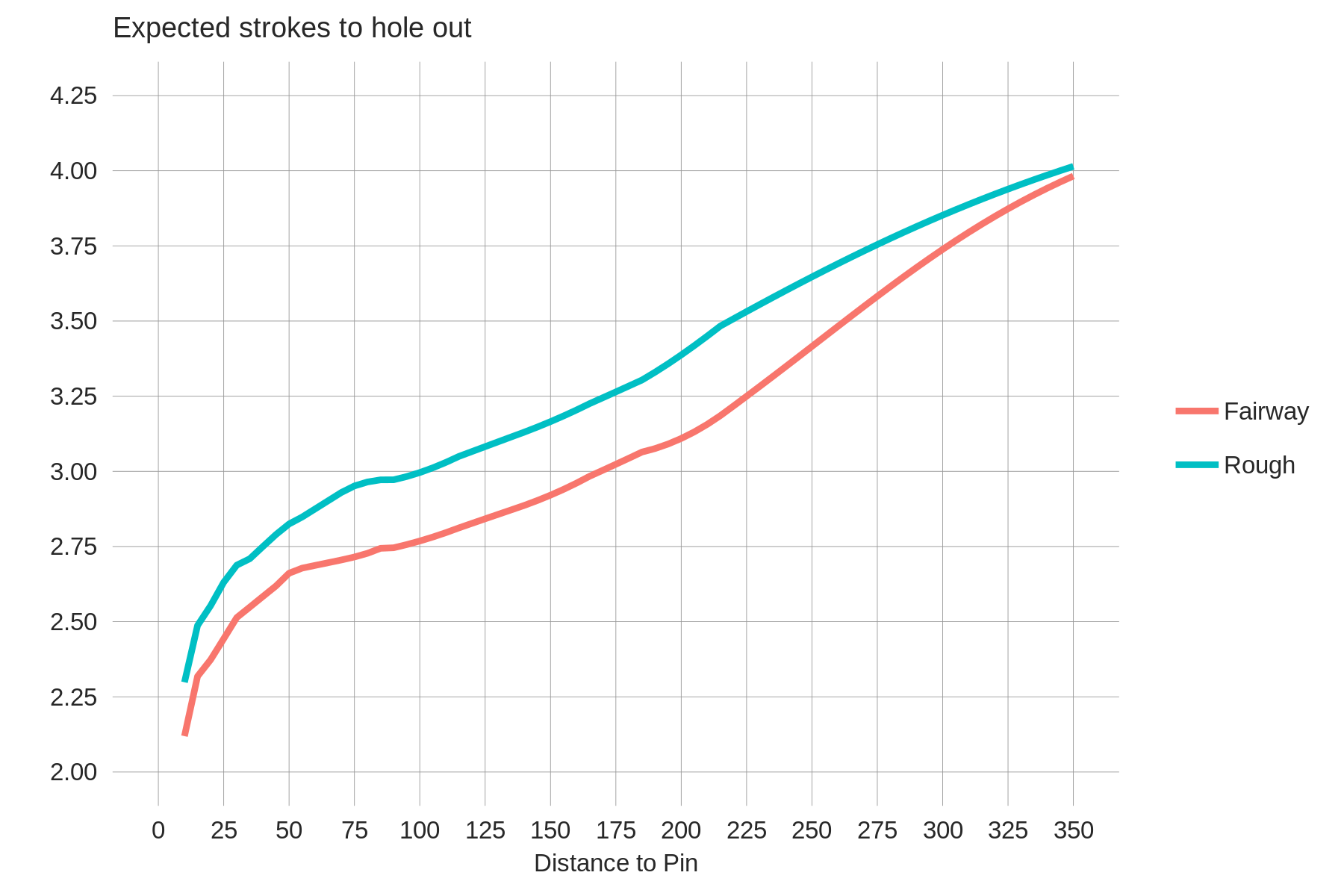
Even if their fairways-hit advantage does not decline substantially as fairway widths shrink, short and accurate golfers could be disadvantaged by hard-to-hit fairways if the 10 or 15 yards they give up to longer hitters is more penalizing from the rough than the fairway. That is, if hitting approach shots from 15 yards further back in the fairway is less of a penalty than hitting approaches from 15 yards back in the rough, then holes with a low overall driving accuracy percentage would tend to disadvantage short players. But, as the graph below (reproduced from this blog post) shows, this isn't true:
For distances in the meat of the approach distribution (75 yards to 225 yards) the expected number of strokes to hole out declines at a similar rate for shots from the fairway or the rough. For example, moving a ball from 175 yards from the pin to 150 yards from the pin is worth about 0.1 strokes whether that move occurs in the fairway or the rough. From distances beyond 225 yards, an additional few yards makes less of a difference from the rough than the fairway (presumably because it's very unlikely to hit the green at those distances from the rough).
The discussion so far could be characterized as an indirect argument for why shorter and accurate players likely don't benefit from wide fairways (and longer, inaccurate players likely don't benefit from narrow fairways). Next, we'll actually look at scoring data for some direct evidence. The table below summarizes the strokes-gained performance of four (overlapping) groups of golfers as a function of the overall driving accuracy percentage on a hole. I've used the quartiles of the DA % distribution to form the bins, so each bin contains the same number of holes (e.g. ~25% of holes on the PGA Tour have a driving accuracy percentage below 58%).
Golfers who are at least 1 standard deviation above the field average in the relevant skill — at the time of
the event — are included in this table (e.g. "long" golfers are >= 1 SD above average in driving distance).
As an example, the first cell tells us that long golfers on average gain 0.036 strokes on holes that have
a DA % below 58%.
Surprisingly (to me), this table shows that longer and less accurate golfers perform
better on narrow holes (the pattern is weak for the inaccurate group), while shorter
and more accurate golfers do the opposite. Alas, the support for this counterintuitive
pattern will be short-lived. As it turns out, holes that have fairways
that are easier to hit also tend to have other, important, characteristics:
Now the strokes-gained averages from the first table take on a different meaning:
holes with low driving accuracy percentages tend to be longer and have smaller
penalties for missing the fairway. The penalty for missing a fairway is calculated
by comparing the hole scores of drives hit into the fairway versus non-fairway locations,
while the rough penalty is calculated by comparing the number of strokes to hole out
from the rough versus the fairway. (There are important details behind these estimates,
which you can read about here.)
One course that fits this mould is Riviera: its par 4s and 5s are well above average in length,
it has
the hardest fairways
to hit on tour, and it consistently has the
smallest penalty
for missing the fairway. And, according to our
course fit tool,
inaccurate golfers play substantially better than their baseline skill at Riviera.
To put this all together, we'll now look at some regressions to get a full picture of which hole characteristics favour certain player types. Shown below are the coefficients from a regression of hole-level strokes-gained on a set of hole characteristics for each of our four groups of golfers:
Let's focus on the first row to gain some understanding of the numbers in this table.
This row contains a set of coefficients from a regression performed only using data for "long" golfers;
the goal is to estimate the impact of each hole characteristic (yardage, missed-fairway penalty, etc)
on the strokes-gained performance of long golfers. Importantly, regression allows us to "control" for
the effect of the other variables;
that is, loosely speaking, the effect of a hole's yardage on long golfers' strokes-gained performance (+0.019) is
estimated by comparing the performance of long golfers on holes of different length but with
similar missed-fairway penalties, rough penalties, etc.
To make the estimates directly comparable to each other, I scale each variable by its standard
deviation (SD). This scaling allows each coefficient to be interpreted as the effect on long golfers' SG
from a 1 SD increase in the relevant variable.
What this means in practice is the following:
the coefficient for yardage
tells us how much the strokes-gained
of long golfers is expected to increase when the yardage of a hole increases by 64 yards (because the SD for hole yardages on
the PGA Tour is 64 yards). Similarly,
the missed-fairway penalty coefficient tell us the expected SG increase from a 0.22 stroke
increase in a hole's missed-fairway penalty.
This scaling makes the magnitudes of the coefficients comparable, as they roughly
represent the difference in expected performance between the median hole in a given characteristic and the 85th percentile hole.
The other three rows display the coefficients from similar regressions
for the remaining three groups of golfers.
The one variable that hasn't been introduced yet is "sd of driving distance", which is a measure how spread out tee shots were (in terms of distance) on a given hole. The course that had the highest average SD in driving distance for its non-par 3 holes was Club de Golf Chapultepec, which makes a lot of sense for anyone who watched those WGC-Mexico events. The asterisks on the table indicate coefficient estimates that were "statistically significant", which, in basic terms, tells you that the estimate cannot be easily explained by noise.
The main takeaways from the table are that the length of the hole and the penalty for missing the fairway are the most important predictors of over or under-performance for a specific group of golfers. Long golfers perform better on long holes, and accurate golfers perform better on holes with large missed-fairway penalties. The field's driving accuracy percentage on a hole, which was our proxy for fairway width, does not have much predictive power for the performance of any group of golfers. If anything, long/inaccurate players perform better with easier-to-hit fairways while short/accurate golfers perform worse on them. The one other variable that did show a sizeable effect was "SD in driving distance" in the long golfer regression. This also seems intuitive. One final remark on interpretation: an effect size of 0.02 strokes would translate to 0.28 strokes per round (if there were 14 non-par 3 holes) — which is a meaningful magnitude when seen in the context of our skill rankings.
Interestingly, the severity of the rough on a hole does not have much predictive power for any group's performance. However, recall that we are controlling for the overall missed-fairway penalty of the hole, which means the rough penalty coefficient is estimated by comparing holes with similar missed-fairway penalties but different rough penalties. This is actually quite tricky to interpret, and it makes me question whether its useful to include both of these variables in the regression. If the rough penalty variable is removed, the missed-fairway penalty coefficients are basically unchanged which is reassuring; if we instead remove the missed-fairway penalty variable, the coefficients on rough penalty are equal to about 50-70% of the missed-fairway penalty estimates shown in the table. There are several possible interpretations of this result, but one interesting interpretation is that when the primary penalty for missing the fairway is ending up in difficult rough, this does not help short, accurate golfers (or hurt long, inaccurate golfers) as much as when the primary penalty for the missed fairway is a non-rough location or a hazard. This provides a nice segue into some concluding thoughts on the limitations of this simple analysis.
The regressions performed above provide predictions for how each group of golfers is expected to perform on each hole. If we aggregate up these predictions by course and compare them to actual performance, we can see where the model's predictions were most off. For long players, the two largest overperformances relative to model predictions occurred at the 2021 U.S. Open at Winged Foot, and the 2019 PGA Championship at Bethpage Black. Given the characteristics of the (non-par 3) holes at Winged Foot, we expected long golfers to gain 0.038 strokes per hole; in fact, they gained 0.099 strokes per hole! A similar story played out at Bethpage: the model predicted +0.02 strokes per hole but long golfers actually gained 0.11. These two tournaments are often pointed to as examples of why narrow fairways and long rough don't favour short, accurate golfers. However, it's not clear whether there are generalizable lessons to be learned from them. One possibility is that the above regressions are too simplistic in that they won't pick up interaction effects: perhaps it is the case that length combined with long rough and difficult-to-hit fairways creates a situation that is especially advantageous for long golfers. Olympia Fields, played in 2020 for the BMW Championship, and Bay Hill are two courses that mostly fit this theory: both are long courses with big rough penalties and hard-to-hit fairways that favour long golfers, however they don't disadvantage accurate golfers. The South Course at Torrey Pines presents a problem however, as it has the required course profile yet doesn't favour long golfers any more than what would be predicted on the basis of its length. Firestone Country Club, whose setup fits the bill perfectly, did not favour long players, or disadvantage accurate players, anymore than expected (using the regression models above) from 2015-2018 at the WGC-Bridgestone. Given these varying results with similar course setups, it's hard to claim that the combination of length, rough, and narrow fairways always act in concert to favour longer players. Two other courses worth pondering are Muirfield Village and East Lake. Muirfield is above average in length and has the worst rough on the PGA Tour, but it tends to favour accuracy over distance. (Muirfield does, however, have an above-average driving accuracy percentage.) East Lake's par 4s and 5s are slightly shorter than Bethpage Black, but has a similar rough penalty and driving accuracy percentage; despite these similarities, East Lake is far from a bomber's paradise. There are surely ways to explain these findings, but, to my eyes, there is not a simple unifying theory.
If the goal is to make course setups more favourable to short and accurate players, increasing (or decreasing) fairway width should not be a top priority. We have provided an indirect argument to support this — the difference in DA % between accurate and inaccurate players is similar regardless of how hard the fairway is to hit — and also direct evidence from hole-level strokes-gained regressions. The analysis here shows that the blueprint for lessening the advantage of bombers is simple: shorten the holes and make the penalty more severe for a wayward drive.
Quick aside — As our loyal readers know,
DG blog posts have a tendency to be technical.
While this is great for those who want to understand the details of an analysis,
it makes some articles less approachable for readers with limited statistics experience.
Therefore, in an attempt to appeal to a wider audience, we've put a non-technical summary
of this article at the bottom of the page.
The starting point will be to think through how we should expect accurate golfers'
advantage in terms of fairways hit to vary as a function
of the width of a fairway. That is, should accurate golfers hit more fairways relative
to inaccurate golfers when the fairway is hard to hit, or when it's easy to hit?
If we were to plot the advantage of accurate golfers as a function of fairway width, we
would expect an upside down U shape: the advantage will be zero at the two extremes (where everyone
is either missing or hitting the fairway), and
will peak somewhere in the middle. Where exactly this advantage peaks will depend on the specific
differences in driving disperson between accurate and inaccurate golfers. For example,
if the difference is that accurate golfers hit fewer foul balls, then we would expect
the peak advantage to occur with relatively wide fairways; if the difference is that accurate golfers hit more
"very straight" drives, then their biggest advantage should be on relatively narrow fairways.
The plot below uses PGA Tour data from 2019-2021 for non-par 3 holes to estimate the driving accuracy difference between accurate and inaccurate golfers as a function of the overall driving accuracy percentage of the hole (we'll use this instead of fairway width, as the conditions of the course — e.g. firmness — can change the "effective" fairway width). Holes are grouped into bins at 5% intervals (e.g. the value at 55% uses holes with a DA % between 52.5% and 57.5%), and accurate golfers are defined to be those at least 1 standard deviation above average in our measure of driving accuracy skill, while inaccurate golfers are at least 1 standard deviation below average in that measure.
The "average" line indicates that across all PGA Tour holes, accurate drivers have a DA % that is 13.6 percentage points higher than inaccurate drivers (73.2% to 59.6% — note that we are counting balls in the intermediate rough as a fairway hit). The data point at 55% tells us that on holes where the field's driving accuracy was between 52.5% and 57.5%, accurate drivers were slightly more than 15 percentage points more likely to hit the fairway than inaccurate drivers. Only 1.5% of holes had an overall driving accuracy percentage below 40%, so they are all placed in the 40% bin. For holes with driving accuracy percentages between 50% and 80%, which characterizes 80% of holes on the PGA Tour, the driving accuracy advantage for accurate players is roughly constant at 13-15%. For holes with a DA % above 0.85 (6% of all holes) this advantage declines sharply; it's likely that a similar decline would be observed for holes below 0.40 DA %, but there simply aren't many PGA Tour holes in that range.
Even if their fairways-hit advantage does not decline substantially as fairway widths shrink, short and accurate golfers could be disadvantaged by hard-to-hit fairways if the 10 or 15 yards they give up to longer hitters is more penalizing from the rough than the fairway. That is, if hitting approach shots from 15 yards further back in the fairway is less of a penalty than hitting approaches from 15 yards back in the rough, then holes with a low overall driving accuracy percentage would tend to disadvantage short players. But, as the graph below (reproduced from this blog post) shows, this isn't true:
For distances in the meat of the approach distribution (75 yards to 225 yards) the expected number of strokes to hole out declines at a similar rate for shots from the fairway or the rough. For example, moving a ball from 175 yards from the pin to 150 yards from the pin is worth about 0.1 strokes whether that move occurs in the fairway or the rough. From distances beyond 225 yards, an additional few yards makes less of a difference from the rough than the fairway (presumably because it's very unlikely to hit the green at those distances from the rough).
The discussion so far could be characterized as an indirect argument for why shorter and accurate players likely don't benefit from wide fairways (and longer, inaccurate players likely don't benefit from narrow fairways). Next, we'll actually look at scoring data for some direct evidence. The table below summarizes the strokes-gained performance of four (overlapping) groups of golfers as a function of the overall driving accuracy percentage on a hole. I've used the quartiles of the DA % distribution to form the bins, so each bin contains the same number of holes (e.g. ~25% of holes on the PGA Tour have a driving accuracy percentage below 58%).
| < 58% | >= 58% and < 66% |
>= 66% and < 75% |
>= 75% | |
|---|---|---|---|---|
| long | 0.036 | 0.028 | 0.028 | 0.019 |
| short | -0.046 | -0.043 | -0.030 | -0.030 |
| accurate | 0.008 | 0.014 | 0.01 | 0.027 |
| inaccurate | -0.038 | -0.042 | -0.038 | -0.047 |
| driving accuracy % | par | yardage | missed-fairway penalty |
rough penalty |
|---|---|---|---|---|
| < 58% | 4.29 | 477 | 0.31 | 0.24 |
| >= 58% & < 66% | 4.23 | 468 | 0.35 | 0.26 |
| >= 66% & < 75% | 4.22 | 459 | 0.37 | 0.26 |
| >= 75% | 4.13 | 437 | 0.42 | 0.30 |
To put this all together, we'll now look at some regressions to get a full picture of which hole characteristics favour certain player types. Shown below are the coefficients from a regression of hole-level strokes-gained on a set of hole characteristics for each of our four groups of golfers:
| yardage | missed-fairway penalty |
rough penalty |
driving accuracy % |
sd of driving distance |
|
|---|---|---|---|---|---|
| long | 0.019* | -0.012* | 0.000 | 0.003 | 0.009* |
| short | -0.014* | 0.009* | 0.002 | -0.001 | -0.004 |
| accurate | -0.016* | 0.020* | -0.004 | -0.004 | -0.006 |
| inaccurate | 0.006 | -0.017* | -0.003 | 0.004 | 0.000 |
The one variable that hasn't been introduced yet is "sd of driving distance", which is a measure how spread out tee shots were (in terms of distance) on a given hole. The course that had the highest average SD in driving distance for its non-par 3 holes was Club de Golf Chapultepec, which makes a lot of sense for anyone who watched those WGC-Mexico events. The asterisks on the table indicate coefficient estimates that were "statistically significant", which, in basic terms, tells you that the estimate cannot be easily explained by noise.
The main takeaways from the table are that the length of the hole and the penalty for missing the fairway are the most important predictors of over or under-performance for a specific group of golfers. Long golfers perform better on long holes, and accurate golfers perform better on holes with large missed-fairway penalties. The field's driving accuracy percentage on a hole, which was our proxy for fairway width, does not have much predictive power for the performance of any group of golfers. If anything, long/inaccurate players perform better with easier-to-hit fairways while short/accurate golfers perform worse on them. The one other variable that did show a sizeable effect was "SD in driving distance" in the long golfer regression. This also seems intuitive. One final remark on interpretation: an effect size of 0.02 strokes would translate to 0.28 strokes per round (if there were 14 non-par 3 holes) — which is a meaningful magnitude when seen in the context of our skill rankings.
Interestingly, the severity of the rough on a hole does not have much predictive power for any group's performance. However, recall that we are controlling for the overall missed-fairway penalty of the hole, which means the rough penalty coefficient is estimated by comparing holes with similar missed-fairway penalties but different rough penalties. This is actually quite tricky to interpret, and it makes me question whether its useful to include both of these variables in the regression. If the rough penalty variable is removed, the missed-fairway penalty coefficients are basically unchanged which is reassuring; if we instead remove the missed-fairway penalty variable, the coefficients on rough penalty are equal to about 50-70% of the missed-fairway penalty estimates shown in the table. There are several possible interpretations of this result, but one interesting interpretation is that when the primary penalty for missing the fairway is ending up in difficult rough, this does not help short, accurate golfers (or hurt long, inaccurate golfers) as much as when the primary penalty for the missed fairway is a non-rough location or a hazard. This provides a nice segue into some concluding thoughts on the limitations of this simple analysis.
The regressions performed above provide predictions for how each group of golfers is expected to perform on each hole. If we aggregate up these predictions by course and compare them to actual performance, we can see where the model's predictions were most off. For long players, the two largest overperformances relative to model predictions occurred at the 2021 U.S. Open at Winged Foot, and the 2019 PGA Championship at Bethpage Black. Given the characteristics of the (non-par 3) holes at Winged Foot, we expected long golfers to gain 0.038 strokes per hole; in fact, they gained 0.099 strokes per hole! A similar story played out at Bethpage: the model predicted +0.02 strokes per hole but long golfers actually gained 0.11. These two tournaments are often pointed to as examples of why narrow fairways and long rough don't favour short, accurate golfers. However, it's not clear whether there are generalizable lessons to be learned from them. One possibility is that the above regressions are too simplistic in that they won't pick up interaction effects: perhaps it is the case that length combined with long rough and difficult-to-hit fairways creates a situation that is especially advantageous for long golfers. Olympia Fields, played in 2020 for the BMW Championship, and Bay Hill are two courses that mostly fit this theory: both are long courses with big rough penalties and hard-to-hit fairways that favour long golfers, however they don't disadvantage accurate golfers. The South Course at Torrey Pines presents a problem however, as it has the required course profile yet doesn't favour long golfers any more than what would be predicted on the basis of its length. Firestone Country Club, whose setup fits the bill perfectly, did not favour long players, or disadvantage accurate players, anymore than expected (using the regression models above) from 2015-2018 at the WGC-Bridgestone. Given these varying results with similar course setups, it's hard to claim that the combination of length, rough, and narrow fairways always act in concert to favour longer players. Two other courses worth pondering are Muirfield Village and East Lake. Muirfield is above average in length and has the worst rough on the PGA Tour, but it tends to favour accuracy over distance. (Muirfield does, however, have an above-average driving accuracy percentage.) East Lake's par 4s and 5s are slightly shorter than Bethpage Black, but has a similar rough penalty and driving accuracy percentage; despite these similarities, East Lake is far from a bomber's paradise. There are surely ways to explain these findings, but, to my eyes, there is not a simple unifying theory.
If the goal is to make course setups more favourable to short and accurate players, increasing (or decreasing) fairway width should not be a top priority. We have provided an indirect argument to support this — the difference in DA % between accurate and inaccurate players is similar regardless of how hard the fairway is to hit — and also direct evidence from hole-level strokes-gained regressions. The analysis here shows that the blueprint for lessening the advantage of bombers is simple: shorten the holes and make the penalty more severe for a wayward drive.
Non-technical Summary
Let’s restate the question — do wider fairways benefit short and accurate golfers?
To begin the analysis, we look at whether any specific fairway width helps accurate players hit relatively more fairways than inaccurate players.
That is, we know accurate players hit about 14% more fairways per round than inaccurate players; does this advantage change when you narrow the fairway? When you widen it?
It turns out their advantage is roughly constant regardless of how hard the fairway is to it (except at the extremes — e.g. when everyone is hitting or missing the fairway — where this advantage inevitably falls).
However, even if their fairways-hit advantage does not decrease as fairways widths narrow, accurate players could still be disadvantaged if the 10 or 15 yards they give up to longer hitters is more penalizing in the rough than in the fairway.
But, we know from a previous blog post (see first plot) that this isn't true: the expected number of strokes to hole out increases at a very similar rate from the fairway and the rough as you move further from the green.
Given these two findings, it seems unlikely that wider fairways would give accurate players an advantage.
Next, we look at actual scoring data. We divide holes into groups based on how hard it is to hit the fairway to see how certain types of golfers (i.e. long or short, accurate or inaccurate) perform on these different sets of holes.
Surprisingly, long and inaccurate golfers perform worse as the fairway gets easier to it, while short and accurate golfers perform better!
However, holes with easy-to-hit fairways also have other features: they tend to be shorter and have larger penalties for missing the fairway.
Once you take this into account, the width of the fairway (or, how difficult it is to hit) has no impact on the over or under-performance of certain golfers.
The two hole characteristics that do have a meaningful effect on the performance of certain groups of golfers are the length of the hole and the penalty for missing the fairway.
This does not rule out that certain combinations of hole characteristics can produce different results. For example, the combination of length, long rough, and narrow fairways is thought by some to be a recipe for a course that favours bombers and hurts short, accurate golfers.
Bethpage Black in 2019 fit this profile and ended up favouring long golfers as much as any course on the PGA Tour from 2019-2021. A similar story played out at Winged Foot at the 2020 U.S. Open.
However, the South Course at Torrey Pines, another long course with penal rough, does not favour long golfers more than you would predict given its length. The same can be said of Firestone Country Club.
There won't be a simple theory to rationalize performance at every course. The key takeaways from this analysis are: 1) long players perform better on holes that are long, while accurate players perform better on holes that have larger penalties for missing the fairway, and 2) the width of the fairway, or how difficult it is to hit, does not meaningfully favour any specific group of golfers.
To begin the analysis, we look at whether any specific fairway width helps accurate players hit relatively more fairways than inaccurate players.
That is, we know accurate players hit about 14% more fairways per round than inaccurate players; does this advantage change when you narrow the fairway? When you widen it?
It turns out their advantage is roughly constant regardless of how hard the fairway is to it (except at the extremes — e.g. when everyone is hitting or missing the fairway — where this advantage inevitably falls).
However, even if their fairways-hit advantage does not decrease as fairways widths narrow, accurate players could still be disadvantaged if the 10 or 15 yards they give up to longer hitters is more penalizing in the rough than in the fairway.
But, we know from a previous blog post (see first plot) that this isn't true: the expected number of strokes to hole out increases at a very similar rate from the fairway and the rough as you move further from the green.
Given these two findings, it seems unlikely that wider fairways would give accurate players an advantage.
Next, we look at actual scoring data. We divide holes into groups based on how hard it is to hit the fairway to see how certain types of golfers (i.e. long or short, accurate or inaccurate) perform on these different sets of holes.
Surprisingly, long and inaccurate golfers perform worse as the fairway gets easier to it, while short and accurate golfers perform better!
However, holes with easy-to-hit fairways also have other features: they tend to be shorter and have larger penalties for missing the fairway.
Once you take this into account, the width of the fairway (or, how difficult it is to hit) has no impact on the over or under-performance of certain golfers.
The two hole characteristics that do have a meaningful effect on the performance of certain groups of golfers are the length of the hole and the penalty for missing the fairway.
This does not rule out that certain combinations of hole characteristics can produce different results. For example, the combination of length, long rough, and narrow fairways is thought by some to be a recipe for a course that favours bombers and hurts short, accurate golfers.
Bethpage Black in 2019 fit this profile and ended up favouring long golfers as much as any course on the PGA Tour from 2019-2021. A similar story played out at Winged Foot at the 2020 U.S. Open.
However, the South Course at Torrey Pines, another long course with penal rough, does not favour long golfers more than you would predict given its length. The same can be said of Firestone Country Club.
There won't be a simple theory to rationalize performance at every course. The key takeaways from this analysis are: 1) long players perform better on holes that are long, while accurate players perform better on holes that have larger penalties for missing the fairway, and 2) the width of the fairway, or how difficult it is to hit, does not meaningfully favour any specific group of golfers.